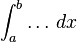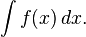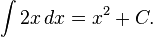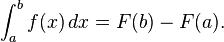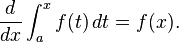Forum Links
Thread Information
Creator
05-14-12 11:05 PM
Post
07-02-13 05:29 PM
Today: 1
Users: 1 unique
Thread Actions


Pokémon Tower Defense!
09-08-12 07:26 AM
 Ktanaqui is Offline
| ID: 649068 | 74 Words
Ktanaqui is Offline
| ID: 649068 | 74 Words
 Ktanaqui is Offline
Ktanaqui is Offline

POSTS: 60/1340
POST EXP: 96116
LVL EXP: 3195687
CP: 1759.5
VIZ: 665676

I am currently stuck on Saffron Gym - I'm playing the Hacked Version so I can gain levels faster. (It would bore me if I had to train as slow as the original.) I have one Level 100 Charizard with Flamethrower and five Gastlys with Shadow Ball and Dark Pulse. Shadow Ball isn't working so I'm going to try Dark Pulse instead. Anyone know where to get a Dark Type Pokemon in this game? |
Affected by 'Laziness Syndrome'
Registered: 09-05-12
Location: Alabama
Last Post: 2369 days
Last Active: 2010 days
10-07-12 11:38 PM
 Singelli is Offline
| ID: 668036 | 46 Words
Singelli is Offline
| ID: 668036 | 46 Words
 Singelli is Offline
Singelli is Offline

POSTS: 613/8698
POST EXP: 1189395
LVL EXP: 53014074
CP: 67331.7
VIZ: 3147678

Wow...now there's something I never would have thought of.. Pokemon and tower defense? Is it as amusing as it sounds? Just the thought of it makes me giggle a little. Is it challenging at all to players who don't play tower defense all that often? Is it challenging at all to players who don't play tower defense all that often? |
| Singelli |
Affected by 'Laziness Syndrome'
Registered: 08-09-12
Location: Alabama
Last Post: 2521 days
Last Active: 2496 days
10-07-12 11:45 PM
 Crazy Li is Offline
| ID: 668043 | 63 Words
Crazy Li is Offline
| ID: 668043 | 63 Words
 Crazy Li is Offline
Crazy Li is Offline

POSTS: 352/1945
POST EXP: 216635
LVL EXP: 5577476
CP: 4056.9
VIZ: 182075

It's extremely challenging, Singelli. I actually have experience with Tower Defense games and I can only get so far in it. It REALLY gets hard after a while. I barely was able to get through the Golden Nugget Bridge because it required a lot of you at that point. I think I only beat the first two gyms and that was about it. |
| Everyone's Favorite Monkey |
Affected by 'Laziness Syndrome'
Registered: 09-21-12
Location: out of this world
Last Post: 3670 days
Last Active: 2026 days
10-08-12 09:40 AM
 Mobouis1 is Offline
| ID: 668226 | 37 Words
Mobouis1 is Offline
| ID: 668226 | 37 Words
 Mobouis1 is Offline
Mobouis1 is Offline

POSTS: 1186/1320
POST EXP: 42307
LVL EXP: 3179325
CP: 343.7
VIZ: 35024

I try this game before at first it was easy, then it start to get way more difficult for me to beat the level. It take me multiple tries to beat one of the more difficult levels.
|
Affected by 'Laziness Syndrome'
Registered: 04-07-12
Last Post: 3963 days
Last Active: 2765 days
10-08-12 10:12 AM
 Stevie 764 is Offline
| ID: 668245 | 176 Words
Stevie 764 is Offline
| ID: 668245 | 176 Words
 Stevie 764 is Offline
Stevie 764 is Offline

POSTS: 2356/2840
POST EXP: 272741
LVL EXP: 10781866
CP: 3982.3
VIZ: 324901

Singeli: Just for me to beat the Cerulean Gym to get my 2nd badge, I had to use the hacked version. Level grinding in the regular game is more than nightmare. It's like... Living in he'll. So hard to level grind. In the hacked version, it is ridiculously easy. Also, even with the hacked version, I gave up at Gym 6 AKA the poison gym.
Guys, there's a PTD2 out on Sam and Dan's website! As of this week, it has a story mode. It is currently at route 29, so you don't have much to do. Every week, it gets updated with another route or whatever it has ready. It updates every week so you may think waiting is boring. But instead of just clicking what level you want to go to unlike PTD1, you actually walk to stuff just like every other non-pokemon fangame. Also, both PTD1 & 2 require you to register by entering your email in the game window, then your password. You can use the password for hacked version, and PTD2. Guys, there's a PTD2 out on Sam and Dan's website! As of this week, it has a story mode. It is currently at route 29, so you don't have much to do. Every week, it gets updated with another route or whatever it has ready. It updates every week so you may think waiting is boring. But instead of just clicking what level you want to go to unlike PTD1, you actually walk to stuff just like every other non-pokemon fangame. Also, both PTD1 & 2 require you to register by entering your email in the game window, then your password. You can use the password for hacked version, and PTD2. |
| Vizzed's former Osu! player and TASer |
Affected by 'Laziness Syndrome'
Registered: 05-28-10
Location: Enfield, CT
Last Post: 2861 days
Last Active: 2854 days
10-08-12 12:39 PM
 Mother3fan5 is Offline
| ID: 668345 | 38 Words
Mother3fan5 is Offline
| ID: 668345 | 38 Words
 Mother3fan5 is Offline
Mother3fan5 is Offline

POSTS: 726/1599
POST EXP: 65090
LVL EXP: 4212088
CP: 1056.8
VIZ: 44071

Ktanaqui : Sorry for the late reply!! There are no dark types in gen 1, so there are no dark types in pokemon tower defense. and my last post was incorrect, they just started with Pokemon tower defense 2. and my last post was incorrect, they just started with Pokemon tower defense 2. |
| the mothcan |
Affected by 'Laziness Syndrome'
Registered: 06-02-12
Last Post: 3133 days
Last Active: 2929 days
12-02-12 07:13 PM
IAMGIYGAS is Offline
| ID: 696429 | 53 Words
POSTS: 9/11
POST EXP: 336
LVL EXP: 2397
CP: 230.6
VIZ: 26728

Yeah. PTD rules. It's real hard though, and why does everyone think leveling up is so hard? Patience dudes.
LIMITED TIME OFFER Those who want to trade for a shiny level 35 tentacruel, PM me. PM ONLY PLEASE Note: this is a little offer. Please don't turn this into a trade offer center. LIMITED TIME OFFER Those who want to trade for a shiny level 35 tentacruel, PM me. PM ONLY PLEASE Note: this is a little offer. Please don't turn this into a trade offer center. |
Affected by 'Laziness Syndrome'
Registered: 06-24-12
Last Post: 3653 days
Last Active: 2866 days
12-02-12 07:20 PM
 earthwarrior is Offline
| ID: 696436 | 19 Words
earthwarrior is Offline
| ID: 696436 | 19 Words
 earthwarrior is Offline
earthwarrior is Offline

POSTS: 395/4807
POST EXP: 221310
LVL EXP: 21874406
CP: 21687.4
VIZ: 123815

I tried it, but forgot to reply. I liked the game. It was interesting that you could catch Pokémon. |
Vizzed's #1 Kid Icarus Uprising Fan! 2nd place in December 2012 VCS! |
Affected by 'Laziness Syndrome'
Registered: 07-03-12
Location: Mars
Last Post: 1925 days
Last Active: 1855 days
12-02-12 11:43 PM
 patar4097 is Offline
| ID: 696526 | 75 Words
patar4097 is Offline
| ID: 696526 | 75 Words
 patar4097 is Offline
patar4097 is Offline

POSTS: 839/5166
POST EXP: 330330
LVL EXP: 26048844
CP: 22170.1
VIZ: 410076

Haven't played it in a while, but it is very fun. It is hard to level up, because it takes so long. It took me quite a while to beat the first gym, and the second one was even harder. But I'm going to get back to it, because I want to play the second one, and I want to have beaten the first one first, because it could have some references to the original. Haven't played it in a while, but it is very fun. It is hard to level up, because it takes so long. It took me quite a while to beat the first gym, and the second one was even harder. But I'm going to get back to it, because I want to play the second one, and I want to have beaten the first one first, because it could have some references to the original. |
Affected by 'Laziness Syndrome'
Registered: 10-28-10
Last Post: 1950 days
Last Active: 763 days
12-07-12 02:10 PM
 haitamchouiekh is Offline
| ID: 698766 | 47 Words
haitamchouiekh is Offline
| ID: 698766 | 47 Words
 haitamchouiekh is Offline
haitamchouiekh is Offline

POSTS: 520/947
POST EXP: 39746
LVL EXP: 1919665
CP: 436.1
VIZ: 44476

i beat it all in the hacked version which is super easy. i caught mewtwo. the trio birds. the fossils. beat all gyms and beat the whole game. but that gamee has viruses. which is why i dont want to play it on my new computer. .. .. |
| Call me Haitam |
Affected by 'Laziness Syndrome'
Registered: 06-02-12
Last Post: 2066 days
Last Active: 1126 days
07-02-13 06:28 AM
 DrakPokeMaster is Offline
| ID: 831509 | 34 Words
DrakPokeMaster is Offline
| ID: 831509 | 34 Words
 DrakPokeMaster is Offline
DrakPokeMaster is Offline

POSTS: 142/427
POST EXP: 21795
LVL EXP: 555406
CP: 1341.4
VIZ: 2746

Very amazing game. I can recall all the times level grinding though. That was a very hard game, but worth it, and now the 2nd is out so there's another adventure to start on. Very amazing game. I can recall all the times level grinding though. That was a very hard game, but worth it, and now the 2nd is out so there's another adventure to start on. |
| Drakkona Darkwynd |
Affected by 'Laziness Syndrome'
Registered: 06-14-13
Last Post: 3189 days
Last Active: 1055 days
07-02-13 06:36 AM
 zelda2 is Offline
| ID: 831516 | 17146 Words
zelda2 is Offline
| ID: 831516 | 17146 Words
 zelda2 is Offline
zelda2 is Offline

POSTS: 1462/1763
POST EXP: -40107
LVL EXP: 4830509
CP: 1466.9
VIZ: 9987

Calculus From Wikipedia, the free encyclopedia This article is about the branch of mathematics. For other uses, see Calculus (disambiguation). CalculusFundamental theoremLimits of functionsContinuityMean value theoremRolle's theorem Differential calculus[show] Integra CalculusFrom Wikipedia, the free encyclopedia This article is about the branch of mathematics. For other uses, see Calculus (disambiguation).
Calculus is the mathematical study of change,[1] in the same way that geometry is the study of shape and algebra is the study of operations and their application to solving equations. It has two major branches, differential calculus (concerning rates of change and slopes of curves), and integral calculus (concerning accumulation of quantities and the areas under curves); these two branches are related to each other by the fundamental theorem of calculus. Both branches make use of the fundamental notions of convergenceof infinite sequences and infinite series to a well-defined limit. Calculus has widespread uses in science, economics, and engineering and can solve many problems that algebraalone cannot. Calculus is a major part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study offunctions and limits, broadly called mathematical analysis. Calculus has historically been called "the calculus of infinitesimals", or "infinitesimal calculus". The word "calculus" comes from Latin (calculus) and means a small stone used for counting. More generally, calculus (plural calculi) refers to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus,calculus of variations, lambda calculus, and process calculus.
History[edit]Main article: History of calculus Ancient[edit]The ancient period introduced some of the ideas that led to integral calculus, but does not seem to have developed these ideas in a rigorous and systematic way. Calculations of volumes and areas, one goal of integral calculus, can be found in the Egyptian Moscow papyrus (c. 1820 BC), but the formulas are simple instructions, with no indication as to method, and some of them lack major components.[2] From the age of Greek mathematics, Eudoxus (c. 408−355 BC) used the method of exhaustion, which foreshadows the concept of the limit, to calculate areas and volumes, while Archimedes (c. 287−212 BC) developed this idea further, inventingheuristics which resemble the methods of integral calculus.[3] The method of exhaustion was later reinvented in China by Liu Hui in the 3rd century AD in order to find the area of a circle.[4] In the 5th century AD, Zu Chongzhi established a method that would later be called Cavalieri's principle to find the volume of a sphere.[5] Medieval[edit]In the 14th century, Indian mathematician Madhava of Sangamagrama and the Kerala school of astronomy and mathematics stated components of calculus such as the Taylor series andinfinite series approximations.[6] Modern[edit]
In Europe, the foundational work was a treatise due to Bonaventura Cavalieri, who argued that volumes and areas should be computed as the sums of the volumes and areas of infinitesimally thin cross-sections. The ideas were similar to Archimedes' inThe Method, but this treatise was lost until the early part of the twentieth century. Cavalieri's work was not well respected since his methods could lead to erroneous results, and the infinitesimal quantities he introduced were disreputable at first. The formal study of calculus brought together Cavalieri's infinitesimals with the calculus of finite differences developed in Europe at around the same time. Pierre de Fermat, claiming that he borrowed from Diophantus, introduced the concept of adequality, which represented equality up to an infinitesimal error term.[8] The combination was achieved by John Wallis, Isaac Barrow, and James Gregory, the latter two proving the second fundamental theorem of calculus around 1670. The product rule and chain rule, the notion of higher derivatives, Taylor series, and analytical functions were introduced by Isaac Newtonin an idiosyncratic notation which he used to solve problems of mathematical physics.[9] In his works, Newton rephrased his ideas to suit the mathematical idiom of the time, replacing calculations with infinitesimals by equivalent geometrical arguments which were considered beyond reproach. He used the methods of calculus to solve the problem of planetary motion, the shape of the surface of a rotating fluid, the oblateness of the earth, the motion of a weight sliding on a cycloid, and many other problems discussed in hisPrincipia Mathematica (1687). In other work, he developed series expansions for functions, including fractional and irrational powers, and it was clear that he understood the principles of the Taylor series. He did not publish all these discoveries, and at this time infinitesimal methods were still considered disreputable.  Gottfried Wilhelm Leibniz was the first to publish his results on the development of calculus. These ideas were arranged into a true calculus of infinitesimals by Gottfried Wilhelm Leibniz, who was originally accused of plagiarism by Newton.[10] He is now regarded as an independent inventor of and contributor to calculus. His contribution was to provide a clear set of rules for working with infinitesimal quantities, allowing the computation of second and higher derivatives, and providing the product rule and chain rule, in their differential and integral forms. Unlike Newton, Leibniz paid a lot of attention to the formalism, often spending days determining appropriate symbols for concepts. Leibniz and Newton are usually both credited with the invention of calculus. Newton was the first to apply calculus to general physics and Leibniz developed much of the notation used in calculus today. The basic insights that both Newton and Leibniz provided were the laws of differentiation and integration, second and higher derivatives, and the notion of an approximating polynomial series. By Newton's time, the fundamental theorem of calculus was known. When Newton and Leibniz first published their results, there was great controversy over which mathematician (and therefore which country) deserved credit. Newton derived his results first, but Leibniz published first. Newton claimed Leibniz stole ideas from his unpublished notes, which Newton had shared with a few members of the Royal Society. This controversy divided English-speaking mathematicians from continental mathematicians for many years, to the detriment of English mathematics. A careful examination of the papers of Leibniz and Newton shows that they arrived at their results independently, with Leibniz starting first with integration and Newton with differentiation. Today, both Newton and Leibniz are given credit for developing calculus independently. It is Leibniz, however, who gave the new discipline its name. Newton called his calculus "the science of fluxions". Since the time of Leibniz and Newton, many mathematicians have contributed to the continuing development of calculus. One of the first and most complete works on finite and infinitesimal analysis was written in 1748 by Maria Gaetana Agnesi.[11] Foundations[edit]In calculus, foundations refers to the rigorous development of a subject from precise axioms and definitions. In early calculus the use of infinitesimal quantities was thought unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle and Bishop Berkeley. Berkeley famously described infinitesimals as the ghosts of departed quantities in his book The Analyst in 1734. A recent study argues that Leibnizian calculus was more solidly grounded than Berkeley's empiricist critique thereof.[12] Working out a rigorous foundation for calculus occupied mathematicians for much of the century following Newton and Leibniz and is still to some extent an active area of research today. Several mathematicians, including Maclaurin, tried to prove the soundness of using infinitesimals, but it would not be until 150 years later when, due to the work of Cauchy and Weierstrass, a way was finally found to avoid mere "notions" of infinitely small quantities. The foundations of differential and integral calculus had been laid. In Cauchy's writing, we find a broad range of foundational approaches, including a definition of continuity in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities. Bernhard Riemann used these ideas to give a precise definition of the integral. It was also during this period that the ideas of calculus were generalized to Euclidean space and the complex plane. In modern mathematics, the foundations of calculus are included in the field of real analysis, which contains full definitions and proofs of the theorems of calculus. The reach of calculus has also been greatly extended. Henri Lebesgue invented measure theory and used it to define integrals of all but the most pathological functions. Laurent Schwartz introduced Distributions, which can be used to take the derivative of any function whatsoever. Limits are not the only rigorous approach to the foundation of calculus. Another way is to use Abraham Robinson's non-standard analysis. Robinson's approach, developed in the 1960s, uses technical machinery from mathematical logic to augment the real number system with infinitesimal and infinite numbers, as in the original Newton-Leibniz conception. The resulting numbers are called hyperreal numbers, and they can be used to give a Leibniz-like development of the usual rules of calculus. Significance[edit]While some of the ideas of calculus had been developed earlier in Egypt, Greece, China, India, Iraq, Persia, and Japan, the modern use of calculus began in Europe, during the 17th century, when Isaac Newton and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to introduce its basic principles. The development of calculus was built on earlier concepts of instantaneous motion and area underneath curves. Applications of differential calculus include computations involving velocity and acceleration, the slope of a curve, and optimization. Applications of integral calculus include computations involving area, volume, arc length, center of mass, work, and pressure. More advanced applications include power series and Fourier series. Calculus is also used to gain a more precise understanding of the nature of space, time, and motion. For centuries, mathematicians and philosophers wrestled with paradoxes involving division by zero or sums of infinitely many numbers. These questions arise in the study of motion and area. The ancient Greek philosopher Zeno of Elea gave several famous examples of such paradoxes. Calculus provides tools, especially the limit and the infinite series, which resolve the paradoxes. Principles[edit]Limits and infinitesimals[edit]Calculus is usually developed by working with very small quantities. Historically, the first method of doing so was by infinitesimals. These are objects which can be treated like numbers but which are, in some sense, "infinitely small". An infinitesimal number dx could be greater than 0, but less than any number in the sequence 1, 1/2, 1/3, ... and less than any positive real number. Any integer multiple of an infinitesimal is still infinitely small, i.e., infinitesimals do not satisfy the Archimedean property. From this point of view, calculus is a collection of techniques for manipulating infinitesimals. This approach fell out of favor in the 19th century because it was difficult to make the notion of an infinitesimal precise. However, the concept was revived in the 20th century with the introduction of non-standard analysis and smooth infinitesimal analysis, which provided solid foundations for the manipulation of infinitesimals. In the 19th century, infinitesimals were replaced by limits. Limits describe the value of a function at a certain input in terms of its values at nearby input. They capture small-scale behavior, just like infinitesimals, but use the ordinary real number system. In this treatment, calculus is a collection of techniques for manipulating certain limits. Infinitesimals get replaced by very small numbers, and the infinitely small behavior of the function is found by taking the limiting behavior for smaller and smaller numbers. Limits are the easiest way to provide rigorous foundations for calculus, and for this reason they are the standard approach. Differential calculus[edit]Main article: Differential calculus Differential calculus is the study of the definition, properties, and applications of the derivative of a function. The process of finding the derivative is calleddifferentiation. Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. By finding the derivative of a function at every point in its domain, it is possible to produce a new function, called the derivative function or just thederivative of the original function. In mathematical jargon, the derivative is alinear operator which inputs a function and outputs a second function. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. (The function it produces turns out to be the doubling function.) The most common symbol for a derivative is an apostrophe-like mark called prime. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function. If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity of the ball. If a function is linear (that is, if the graph of the function is a straight line), then the function can be written as y = mx + b, where x is the independent variable, y is the dependent variable, b is the y-intercept, and: This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in ydivided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point abecause it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero: Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f. Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function.  The derivative f′(x) of a curve at a point is the slope of the line tangent to that curve at that point. This slope is determined by considering the limiting value of the slopes of secant lines. Here the function involved (drawn in red) is f(x) = x3 − x. The tangent line (in green) which passes through the point (−3/2, −15/8) has a slope of 23/4. Note that the vertical and horizontal scales in this image are different. The slope of tangent line to the squaring function at the point (3,9) is 6, that is to say, it is going up six times as fast as it is going to the right. The limit process just described can be performed for any point in the domain of the squaring function. This defines the derivative function of the squaring function, or just the derivative of the squaring function for short. A similar computation to the one above shows that the derivative of the squaring function is the doubling function. Leibniz notation[edit]Main article: Leibniz's notation A common notation, introduced by Leibniz, for the derivative in the example above is In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example: In this usage, the dx in the denominator is read as "with respect to x". Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real numbers; although it is possible to avoid such manipulations, they are sometimes notationally convenient in expressing operations such as the total derivative. Integral calculus[edit]Main article: Integral Integral calculus is the study of the definitions, properties, and applications of two related concepts, the indefinite integral and thedefinite integral. The process of finding the value of an integral is called integration. In technical language, integral calculus studies two related linear operators. The indefinite integral is the antiderivative, the inverse operation to the derivative. F is an indefinite integral of f when f is a derivative of F. (This use of lower- and upper-case letters for a function and its indefinite integral is common in calculus.) The definite integral inputs a function and outputs a number, which gives the algebraic sum of areas between the graph of the input and the x-axis. The technical definition of the definite integral is the limit of a sum of areas of rectangles, called a Riemann sum. A motivating example is the distances traveled in a given time. If the speed is constant, only multiplication is needed, but if the speed changes, then we need a more powerful method of finding the distance. One such method is to approximate the distance traveled by breaking up the time into many short intervals of time, then multiplying the time elapsed in each interval by one of the speeds in that interval, and then taking the sum (a Riemann sum) of the approximate distance traveled in each interval. The basic idea is that if only a short time elapses, then the speed will stay more or less the same. However, a Riemann sum only gives an approximation of the distance traveled. We must take the limit of all such Riemann sums to find the exact distance traveled. If f(x) in the diagram on the left represents speed as it varies over time, the distance traveled (between the times represented by a and b) is the area of the shaded region s. To approximate that area, an intuitive method would be to divide up the distance between a and b into a number of equal segments, the length of each segment represented by the symbol Δx. For each small segment, we can choose one value of the function f(x). Call that value h. Then the area of the rectangle with base Δxand height h gives the distance (time Δx multiplied by speed h) traveled in that segment. Associated with each segment is the average value of the function above it, f(x)=h. The sum of all such rectangles gives an approximation of the area between the axis and the curve, which is an approximation of the total distance traveled. A smaller value for Δx will give more rectangles and in most cases a better approximation, but for an exact answer we need to take a limit as Δxapproaches zero. The symbol of integration is and is read "the integral from a to b of f-of-x with respect to x." The Leibniz notation dx is intended to suggest dividing the area under the curve into an infinite number of rectangles, so that their width Δx becomes the infinitesimally small dx. In a formulation of the calculus based on limits, the notation is to be understood as an operator that takes a function as an input and gives a number, the area, as an output. The terminating differential, dx, is not a number, and is not being multiplied by f(x), although, serving as a reminder of the Δx limit definition, it can be treated as such in symbolic manipulations of the integral. Formally, the differential indicates the variable over which the function is integrated and serves as a closing bracket for the integration operator. The indefinite integral, or antiderivative, is written: Functions differing by only a constant have the same derivative, and it can be shown that the antiderivative of a given function is actually a family of functions differing only by a constant. Since the derivative of the function y = x² + C, where C is any constant, is y′ = 2x, the antiderivative of the latter given by: The unspecified constant C present in the indefinite integral or antiderivative is known as the constant of integration. Fundamental theorem[edit]Main article: Fundamental theorem of calculus The fundamental theorem of calculus states that differentiation and integration are inverse operations. More precisely, it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition of a definite integral, the Fundamental Theorem of Calculus provides a practical way of computing definite integrals. It can also be interpreted as a precise statement of the fact that differentiation is the inverse of integration. The Fundamental Theorem of Calculus states: If a function f is continuous on the interval [a, b ] and if F is a function whose derivative isf on the interval (a, b ), then Furthermore, for every x in the interval (a, b), This realization, made by both Newton and Leibniz, who based their results on earlier work by Isaac Barrow, was key to the massive proliferation of analytic results after their work became known. The fundamental theorem provides an algebraic method of computing many definite integrals—without performing limit processes—by finding formulas for antiderivatives. It is also a prototype solution of adifferential equation. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences. Applications[edit] The logarithmic spiral of the Nautilus shellis a classical image used to depict the growth and change related to calculus Calculus is used in every branch of the physical sciences, actuarial science, computer science, statistics, engineering, economics, business, medicine, demography, and in other fields wherever a problem can be mathematically modeled and an optimal solution is desired. It allows one to go from (non-constant) rates of change to the total change or vice versa, and many times in studying a problem we know one and are trying to find the other. Physics makes particular use of calculus; all concepts in classical mechanics andelectromagnetism are interrelated through calculus. The mass of an object of known density, the moment of inertia of objects, as well as the total energy of an object within a conservative field can be found by the use of calculus. An example of the use of calculus in mechanics is Newton's second law of motion historically stated it expressly uses the term "rate of change" which refers to the derivative saying The rate of change of momentum of a body is equal to the resultant force acting on the body and is in the same direction.Commonly expressed today as Force = Mass × acceleration, it involves differential calculus because acceleration is the time derivative of velocity or second time derivative of trajectory or spatial position. Starting from knowing how an object is accelerating, we use calculus to derive its path. Maxwell's theory of electromagnetism and Einstein's theory of general relativity are also expressed in the language of differential calculus. Chemistry also uses calculus in determining reaction rates and radioactive decay. In biology, population dynamics starts with reproduction and death rates to model population changes. Calculus can be used in conjunction with other mathematical disciplines. For example, it can be used with linear algebra to find the "best fit" linear approximation for a set of points in a domain. Or it can be used in probability theory to determine the probability of a continuous random variable from an assumed density function. In analytic geometry, the study of graphs of functions, calculus is used to find high points and low points (maxima and minima), slope, concavity and inflection points. Green's Theorem, which gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, is applied in an instrument known as a planimeter, which is used to calculate the area of a flat surface on a drawing. For example, it can be used to calculate the amount of area taken up by an irregularly shaped flower bed or swimming pool when designing the layout of a piece of property. Discrete Green's Theorem, which gives the relationship between a double integral of a function around a simple closed rectangular curveC and a linear combination of the antiderivative's values at corner points along the edge of the curve, allows fast calculation of sums of values in rectangular domains. For example, it can be used to efficiently calculate sums of rectangular domains in images, in order to rapidly extract features and detect object - see also the summed area table algorithm. In the realm of medicine, calculus can be used to find the optimal branching angle of a blood vessel so as to maximize flow. From the decay laws for a particular drug's elimination from the body, it's used to derive dosing laws. In nuclear medicine, it's used to build models of radiation transport in targeted tumor therapies. In economics, calculus allows for the determination of maximal profit by providing a way to easily calculate both marginal cost andmarginal revenue. Calculus is also used to find approximate solutions to equations; in practice it's the standard way to solve differential equations and do root finding in most applications. Examples are methods such as Newton's method, fixed point iteration, and linear approximation. For instance, spacecraft use a variation of the Euler method to approximate curved courses within zero gravity environments. See also[edit]Main article: Outline of calculus Lists[edit]
Related topics[edit]
References[edit]Notes[edit]
Books[edit]
Other resources[edit]Further reading[edit]
Online books[edit]
External links[edit]
Navigation menuNavigationToolboxPrint/exportLanguages
Series[show] Vector calculus[show] Multivariable calculus[show] Specialized calculi[show] vte Calculus is the mathematical study of change,[1] in the same way that geometry is the study of shape and algebra is the study of operations and their application to solving equations. It has two major branches, differential calculus (concerning rates of change and slopes of curves), and integral calculus (concerning accumulation of quantities and the areas under curves); these two branches are related to each other by the fundamental theorem of calculus. Both branches make use of the fundamental notions of convergenceof infinite sequences and infinite series to a well-defined limit. Calculus has widespread uses in science, economics, and engineering and can solve many problems that algebraalone cannot. Calculus is a major part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study offunctions and limits, broadly called mathematical analysis. Calculus has historically been called "the calculus of infinitesimals", or "infinitesimal calculus". The word "calculus" comes from Latin (calculus) and means a small stone used for counting. More generally, calculus (plural calculi) refers to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus,calculus of variations, lambda calculus, and process calculus. Contents [hide] 1History1.1Ancient1.2Medieval1.3Modern1.4Foundations1.5Significance2Principles2.1Limits and infinitesimals2.2Differential calculus2.3Leibniz notation2.4Integral calculus2.5Fundamental theorem3Applications4See also4.1Lists4.2Related topics5References5.1Notes5.2Books6Other resources6.1Further reading6.2Online books7External linksHistory[edit] Main article: History of calculus Ancient[edit] Isaac Newton developed the use of calculus in his laws of motion andgravitation. The ancient period introduced some of the ideas that led to integral calculus, but does not seem to have developed these ideas in a rigorous and systematic way. Calculations of volumes and areas, one goal of integral calculus, can be found in the EgyptianMoscow papyrus (c. 1820 BC), but the formulas are simple instructions, with no indication as to method, and some of them lack major components.[2] From the age of Greek mathematics, Eudoxus (c. 408−355 BC) used the method of exhaustion, which foreshadows the concept of the limit, to calculate areas and volumes, while Archimedes (c. 287−212 BC) developed this idea further, inventingheuristics which resemble the methods of integral calculus.[3] The method of exhaustion was later reinvented in China by Liu Hui in the 3rd century AD in order to find the area of a circle.[4] In the 5th century AD, Zu Chongzhi established a method that would later be called Cavalieri's principle to find the volume of a sphere.[5] Medieval[edit] In the 14th century, Indian mathematician Madhava of Sangamagrama and the Kerala school of astronomy and mathematics stated components of calculus such as the Taylor series andinfinite series approximations.[6] Modern[edit]"The calculus was the first achievement of modern mathematics and it is difficult to overestimate its importance. I think it defines more unequivocally than anything else the inception of modern mathematics, and the system of mathematical analysis, which is its logical development, still constitutes the greatest technical advance in exact thinking." —John von Neumann[7] In Europe, the foundational work was a treatise due to Bonaventura Cavalieri, who argued that volumes and areas should be computed as the sums of the volumes and areas of infinitesimally thin cross-sections. The ideas were similar to Archimedes' inThe Method, but this treatise was lost until the early part of the twentieth century. Cavalieri's work was not well respected since his methods could lead to erroneous results, and the infinitesimal quantities he introduced were disreputable at first. The formal study of calculus brought together Cavalieri's infinitesimals with the calculus of finite differences developed in Europe at around the same time. Pierre de Fermat, claiming that he borrowed from Diophantus, introduced the concept of adequality, which represented equality up to an infinitesimal error term.[8] The combination was achieved by John Wallis, Isaac Barrow, and James Gregory, the latter two proving the second fundamental theorem of calculus around 1670. The product rule and chain rule, the notion of higher derivatives, Taylor series, and analytical functions were introduced by Isaac Newtonin an idiosyncratic notation which he used to solve problems of mathematical physics.[9] In his works, Newton rephrased his ideas to suit the mathematical idiom of the time, replacing calculations with infinitesimals by equivalent geometrical arguments which were considered beyond reproach. He used the methods of calculus to solve the problem of planetary motion, the shape of the surface of a rotating fluid, the oblateness of the earth, the motion of a weight sliding on a cycloid, and many other problems discussed in hisPrincipia Mathematica (1687). In other work, he developed series expansions for functions, including fractional and irrational powers, and it was clear that he understood the principles of the Taylor series. He did not publish all these discoveries, and at this time infinitesimal methods were still considered disreputable. Gottfried Wilhelm Leibniz was the first to publish his results on the development of calculus. These ideas were arranged into a true calculus of infinitesimals by Gottfried Wilhelm Leibniz, who was originally accused of plagiarism by Newton.[10] He is now regarded as an independent inventor of and contributor to calculus. His contribution was to provide a clear set of rules for working with infinitesimal quantities, allowing the computation of second and higher derivatives, and providing the product rule and chain rule, in their differential and integral forms. Unlike Newton, Leibniz paid a lot of attention to the formalism, often spending days determining appropriate symbols for concepts. Leibniz and Newton are usually both credited with the invention of calculus. Newton was the first to apply calculus to general physics and Leibniz developed much of the notation used in calculus today. The basic insights that both Newton and Leibniz provided were the laws of differentiation and integration, second and higher derivatives, and the notion of an approximating polynomial series. By Newton's time, the fundamental theorem of calculus was known. When Newton and Leibniz first published their results, there was great controversy over which mathematician (and therefore which country) deserved credit. Newton derived his results first, but Leibniz published first. Newton claimed Leibniz stole ideas from his unpublished notes, which Newton had shared with a few members of the Royal Society. This controversy divided English-speaking mathematicians from continental mathematicians for many years, to the detriment of English mathematics. A careful examination of the papers of Leibniz and Newton shows that they arrived at their results independently, with Leibniz starting first with integration and Newton with differentiation. Today, both Newton and Leibniz are given credit for developing calculus independently. It is Leibniz, however, who gave the new discipline its name. Newton called his calculus "the science of fluxions". Since the time of Leibniz and Newton, many mathematicians have contributed to the continuing development of calculus. One of the first and most complete works on finite and infinitesimal analysis was written in 1748 by Maria Gaetana Agnesi.[11] Maria Gaetana Agnesi Foundations[edit] In calculus, foundations refers to the rigorous development of a subject from precise axioms and definitions. In early calculus the use of infinitesimal quantities was thought unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle and Bishop Berkeley. Berkeley famously described infinitesimals as the ghosts of departed quantities in his book The Analyst in 1734. A recent study argues that Leibnizian calculus was more solidly grounded than Berkeley's empiricist critique thereof.[12] Working out a rigorous foundation for calculus occupied mathematicians for much of the century following Newton and Leibniz and is still to some extent an active area of research today. Several mathematicians, including Maclaurin, tried to prove the soundness of using infinitesimals, but it would not be until 150 years later when, due to the work of Cauchy and Weierstrass, a way was finally found to avoid mere "notions" of infinitely small quantities. The foundations of differential and integral calculus had been laid. In Cauchy's writing, we find a broad range of foundational approaches, including a definition of continuity in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities. Bernhard Riemann used these ideas to give a precise definition of the integral. It was also during this period that the ideas of calculus were generalized to Euclidean space and the complex plane. In modern mathematics, the foundations of calculus are included in the field of real analysis, which contains full definitions and proofs of the theorems of calculus. The reach of calculus has also been greatly extended. Henri Lebesgue invented measure theory and used it to define integrals of all but the most pathological functions. Laurent Schwartz introduced Distributions, which can be used to take the derivative of any function whatsoever. Limits are not the only rigorous approach to the foundation of calculus. Another way is to use Abraham Robinson's non-standard analysis. Robinson's approach, developed in the 1960s, uses technical machinery from mathematical logic to augment the real number system with infinitesimal and infinite numbers, as in the original Newton-Leibniz conception. The resulting numbers are called hyperreal numbers, and they can be used to give a Leibniz-like development of the usual rules of calculus. Significance[edit] While some of the ideas of calculus had been developed earlier in Egypt, Greece, China, India, Iraq, Persia, and Japan, the modern use of calculus began in Europe, during the 17th century, when Isaac Newton and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to introduce its basic principles. The development of calculus was built on earlier concepts of instantaneous motion and area underneath curves. Applications of differential calculus include computations involving velocity and acceleration, the slope of a curve, and optimization. Applications of integral calculus include computations involving area, volume, arc length, center of mass, work, and pressure. More advanced applications include power series and Fourier series. Calculus is also used to gain a more precise understanding of the nature of space, time, and motion. For centuries, mathematicians and philosophers wrestled with paradoxes involving division by zero or sums of infinitely many numbers. These questions arise in the study of motion and area. The ancient GreekphilosopherZeno of Elea gave several famous examples of such paradoxes. Calculus provides tools, especially the limit and the infinite series, which resolve the paradoxes. Principles[edit]Limits and infinitesimals[edit] Main articles: Limit of a function, Infinitesimal, and Infinitesimal Calculus Calculus is usually developed by working with very small quantities. Historically, the first method of doing so was by infinitesimals. These are objects which can be treated like numbers but which are, in some sense, "infinitely small". An infinitesimal number dx could be greater than 0, but less than any number in the sequence 1, 1/2, 1/3, ... and less than any positive real number. Any integer multiple of an infinitesimal is still infinitely small, i.e., infinitesimals do not satisfy the Archimedean property. From this point of view, calculus is a collection of techniques for manipulating infinitesimals. This approach fell out of favor in the 19th century because it was difficult to make the notion of an infinitesimal precise. However, the concept was revived in the 20th century with the introduction of non-standard analysis and smooth infinitesimal analysis, which provided solid foundations for the manipulation of infinitesimals. In the 19th century, infinitesimals were replaced by limits. Limits describe the value of a function at a certain input in terms of its values at nearby input. They capture small-scale behavior, just like infinitesimals, but use the ordinary real number system. In this treatment, calculus is a collection of techniques for manipulating certain limits. Infinitesimals get replaced by very small numbers, and the infinitely small behavior of the function is found by taking the limiting behavior for smaller and smaller numbers. Limits are the easiest way to provide rigorous foundations for calculus, and for this reason they are the standard approach. Differential calculus[edit] Main article: Differential calculus Tangent line at (x, f(x)). The derivative f′(x) of a curve at a point is the slope (rise over run) of the line tangent to that curve at that point. Differential calculus is the study of the definition, properties, and applications of the derivative of a function. The process of finding the derivative is calleddifferentiation. Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. By finding the derivative of a function at every point in its domain, it is possible to produce a new function, called the derivative function or just thederivative of the original function. In mathematical jargon, the derivative is alinear operator which inputs a function and outputs a second function. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. (The function it produces turns out to be the doubling function.) The most common symbol for a derivative is an apostrophe-like mark called prime. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function. If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity of the ball. If a function is linear (that is, if the graph of the function is a straight line), then the function can be written as y = mx + b, where x is the independent variable, y is the dependent variable, b is the y-intercept, and: This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in ydivided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point abecause it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero: Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f. Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function. The derivative f′(x) of a curve at a point is the slope of the line tangent to that curve at that point. This slope is determined by considering the limiting value of the slopes of secant lines. Here the function involved (drawn in red) is f(x) = x3 − x. The tangent line (in green) which passes through the point (−3/2, −15/8) has a slope of 23/4. Note that the vertical and horizontal scales in this image are different. The slope of tangent line to the squaring function at the point (3,9) is 6, that is to say, it is going up six times as fast as it is going to the right. The limit process just described can be performed for any point in the domain of the squaring function. This defines the derivative function of the squaring function, or just the derivative of the squaring function for short. A similar computation to the one above shows that the derivative of the squaring function is the doubling function. Leibniz notation[edit] Main article: Leibniz's notation A common notation, introduced by Leibniz, for the derivative in the example above is In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example: In this usage, the dx in the denominator is read as "with respect to x". Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real numbers; although it is possible to avoid such manipulations, they are sometimes notationally convenient in expressing operations such as the total derivative. Integral calculus[edit] Main article: Integral Integral calculus is the study of the definitions, properties, and applications of two related concepts, the indefinite integral and thedefinite integral. The process of finding the value of an integral is called integration. In technical language, integral calculus studies two related linear operators. The indefinite integral is the antiderivative, the inverse operation to the derivative. F is an indefinite integral of f when f is a derivative of F. (This use of lower- and upper-case letters for a function and its indefinite integral is common in calculus.) The definite integral inputs a function and outputs a number, which gives the algebraic sum of areas between the graph of the input and the x-axis. The technical definition of the definite integral is the limit of a sum of areas of rectangles, called a Riemann sum. A motivating example is the distances traveled in a given time. If the speed is constant, only multiplication is needed, but if the speed changes, then we need a more powerful method of finding the distance. One such method is to approximate the distance traveled by breaking up the time into many short intervals of time, then multiplying the time elapsed in each interval by one of the speeds in that interval, and then taking the sum (a Riemann sum) of the approximate distance traveled in each interval. The basic idea is that if only a short time elapses, then the speed will stay more or less the same. However, a Riemann sum only gives an approximation of the distance traveled. We must take the limit of all such Riemann sums to find the exact distance traveled. Integration can be thought of as measuring the area under a curve, defined by f(x), between two points (here a and b). If f(x) in the diagram on the left represents speed as it varies over time, the distance traveled (between the times represented by a and b) is the area of the shaded region s. To approximate that area, an intuitive method would be to divide up the distance between a and b into a number of equal segments, the length of each segment represented by the symbol Δx. For each small segment, we can choose one value of the function f(x). Call that value h. Then the area of the rectangle with base Δxand height h gives the distance (time Δx multiplied by speed h) traveled in that segment. Associated with each segment is the average value of the function above it, f(x)=h. The sum of all such rectangles gives an approximation of the area between the axis and the curve, which is an approximation of the total distance traveled. A smaller value for Δx will give more rectangles and in most cases a better approximation, but for an exact answer we need to take a limit as Δxapproaches zero. The symbol of integration is , an elongated S (the S stands for "sum"). The definite integral is written as: and is read "the integral from a to b of f-of-x with respect to x." The Leibniz notation dx is intended to suggest dividing the area under the curve into an infinite number of rectangles, so that their width Δx becomes the infinitesimally small dx. In a formulation of the calculus based on limits, the notation is to be understood as an operator that takes a function as an input and gives a number, the area, as an output. The terminating differential, dx, is not a number, and is not being multiplied by f(x), although, serving as a reminder of the Δx limit definition, it can be treated as such in symbolic manipulations of the integral. Formally, the differential indicates the variable over which the function is integrated and serves as a closing bracket for the integration operator. The indefinite integral, or antiderivative, is written: Functions differing by only a constant have the same derivative, and it can be shown that the antiderivative of a given function is actually a family of functions differing only by a constant. Since the derivative of the function y = x² + C, where C is any constant, is y′ = 2x, the antiderivative of the latter given by: The unspecified constant C present in the indefinite integral or antiderivative is known as the constant of integration. Fundamental theorem[edit] Main article: Fundamental theorem of calculus The fundamental theorem of calculus states that differentiation and integration are inverse operations. More precisely, it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition of a definite integral, the Fundamental Theorem of Calculus provides a practical way of computing definite integrals. It can also be interpreted as a precise statement of the fact that differentiation is the inverse of integration. The Fundamental Theorem of Calculus states: If a function f is continuous on the interval [a, b ] and if F is a function whose derivative isf on the interval (a, b ), then Furthermore, for every x in the interval (a, b), This realization, made by both Newton and Leibniz, who based their results on earlier work by Isaac Barrow, was key to the massive proliferation of analytic results after their work became known. The fundamental theorem provides an algebraic method of computing many definite integrals—without performing limit processes—by finding formulas for antiderivatives. It is also a prototype solution of adifferential equation. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences. Applications[edit] The logarithmic spiral of the Nautilus shellis a classical image used to depict the growth and change related to calculus Calculus is used in every branch of the physical sciences, actuarial science, computer science, statistics, engineering, economics, business, medicine, demography, and in other fields wherever a problem can be mathematically modeled and an optimal solution is desired. It allows one to go from (non-constant) rates of change to the total change or vice versa, and many times in studying a problem we know one and are trying to find the other. Physics makes particular use of calculus; all concepts in classical mechanics andelectromagnetism are interrelated through calculus. The mass of an object of known density, the moment of inertia of objects, as well as the total energy of an object within a conservative field can be found by the use of calculus. An example of the use of calculus in mechanics is Newton's second law of motion: historically stated it expressly uses the term "rate of change" which refers to the derivative saying Therate of changeof momentum of a body is equal to the resultant force acting on the body and is in the same direction.Commonly expressed today as Force = Mass × acceleration, it involves differential calculus because acceleration is the time derivative of velocity or second time derivative of trajectory or spatial position. Starting from knowing how an object is accelerating, we use calculus to derive its path. Maxwell's theory of electromagnetism and Einstein's theory of general relativity are also expressed in the language of differential calculus. Chemistry also uses calculus in determining reaction rates and radioactive decay. In biology, population dynamics starts with reproduction and death rates to model population changes. Calculus can be used in conjunction with other mathematical disciplines. For example, it can be used with linear algebra to find the "best fit" linear approximation for a set of points in a domain. Or it can be used in probability theory to determine the probability of a continuous random variable from an assumed density function. In analytic geometry, the study of graphs of functions, calculus is used to find high points and low points (maxima and minima), slope, concavity and inflection points. Green's Theorem, which gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, is applied in an instrument known as a planimeter, which is used to calculate the area of a flat surface on a drawing. For example, it can be used to calculate the amount of area taken up by an irregularly shaped flower bed or swimming pool when designing the layout of a piece of property. Discrete Green's Theorem, which gives the relationship between a double integral of a function around a simple closed rectangular curveC and a linear combination of the antiderivative's values at corner points along the edge of the curve, allows fast calculation of sums of values in rectangular domains. For example, it can be used to efficiently calculate sums of rectangular domains in images, in order to rapidly extract features and detect object - see also the summed area table algorithm. In the realm of medicine, calculus can be used to find the optimal branching angle of a blood vessel so as to maximize flow. From the decay laws for a particular drug's elimination from the body, it's used to derive dosing laws. In nuclear medicine, it's used to build models of radiation transport in targeted tumor therapies. In economics, calculus allows for the determination of maximal profit by providing a way to easily calculate both marginal cost andmarginal revenue. Calculus is also used to find approximate solutions to equations; in practice it's the standard way to solve differential equations and do root finding in most applications. Examples are methods such as Newton's method, fixed point iteration, and linear approximation. For instance, spacecraft use a variation of the Euler method to approximate curved courses within zero gravity environments. See also[edit] Mathematics portalAnalysis portal Main article: Outline of calculus Lists[edit]List of calculus topicsList of derivatives and integrals in alternative calculiList of differentiation identitiesPublications in calculusTable of integralsRelated topics[edit]Calculus of finite differencesCalculus with polynomialsComplex analysisDifferential equationDifferential geometryElementary Calculus: An Infinitesimal ApproachFourier seriesIntegral equationMathematical analysisMultivariable calculusNon-classical analysisNon-standard analysisNon-standard calculusPrecalculus (mathematical education)Product integralStochastic calculusTaylor seriesReferences[edit]Notes[edit] ^Latorre, Donald R.; Kenelly, John W.; Reed, Iris B.; Biggers, Sherry (2007), Calculus Concepts: An Applied Approach to the Mathematics of Change, Cengage Learning, p. 2, ISBN0-618-78981-2, Chapter 1, p 2^Morris Kline, Mathematical thought from ancient to modern times, Vol. I^Archimedes, Method, in The Works of ArchimedesISBN 978-0-521-66160-7^Dun, Liu; Fan, Dainian; Cohen, Robert Sonné (1966). A comparison of Archimdes' and Liu Hui's studies of circles. Chinese studies in the history and philosophy of science and technology 130. Springer. p. 279. ISBN0-7923-3463-9., Chapter , p. 279^Zill, Dennis G.; Wright, Scott; Wright, Warren S. (2009).Calculus: Early Transcendentals (3 ed.). Jones & Bartlett Learning. p. xxvii. ISBN0-7637-5995-3., Extract of page 27^http://www-history.mcs.st-andrews.ac.uk/HistTopics/Indian_mathematics.html^von Neumann, J., "The Mathematician", in Heywood, R. B., ed.,The Works of the Mind, University of Chicago Press, 1947, pp. 180–196. Reprinted in Bródy, F., Vámos, T., eds., The Neumann Compedium, World Scientific Publishing Co. Pte. Ltd., 1995,ISBN 981-02-2201-7, pp. 618–626.^André Weil: Number theory. An approach through history. From Hammurapi to Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0-8176-4565-9, p. 28.^Donald Allen: Calculus,http://www.math.tamu.edu/~dallen/history/calc1/calc1.html^Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscr Books[edit] Larson, Ron, Bruce H. Edwards (2010). "Calculus", 9th ed., Brooks Cole Cengage Learning. ISBN 978-0-547-16702-2McQuarrie, Donald A. (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 978-1-891389-24-5Stewart, James (2008). Calculus: Early Transcendentals, 6th ed., Brooks Cole Cengage Learning. ISBN 978-0-495-01166-8Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano (2008), "Calculus", 11th ed., Addison-Wesley. ISBN 0-321-48987-X Other resources[edit]Further reading[edit] Boyer, Carl Benjamin (1949). The History of the Calculus and its Conceptual Development. Hafner. Dover edition 1959, ISBN 0-486-60509-4Courant, RichardISBN 978-3-540-65058-4Introduction to calculus and analysis 1.Edmund Landau. ISBN 0-8218-2830-4Differential and Integral Calculus, American Mathematical Society.Robert A. Adams. (1999). ISBN 978-0-201-39607-2Calculus: A complete course.Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7.John Lane Bell: A Primer of Infinitesimal Analysis, Cambridge University Press, 1998. ISBN 978-0-521-62401-5. Uses synthetic differential geometry and nilpotent infinitesimals.Florian Cajori, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), pp. 1–46.Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton Univ. Press, 2004.Cliff Pickover. (2003). ISBN 978-0-471-26987-8Calculus and Pizza: A Math Cookbook for the Hungry Mind.Michael Spivak. (September 1994). ISBN 978-0-914098-89-8Calculus. Publish or Perish publishing.Tom M. Apostol. (1967). ISBN 978-0-471-00005-1Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley.Tom M. Apostol. (1969). ISBN 978-0-471-00007-5Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley.Silvanus P. Thompson and Martin Gardner. (1998). ISBN 978-0-312-18548-0Calculus Made Easy.Mathematical Association of America. (1988). Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.Thomas/Finney. (1996). ISBN 978-0-201-53174-9Calculus and Analytic geometry 9th, Addison Wesley.Weisstein, Eric W. "Second Fundamental Theorem of Calculus."From MathWorld—A Wolfram Web Resource.Howard Anton,Irl Bivens,Stephen Davis:"Calculus",John Willey and Sons Pte. Ltd.,2002.ISBN 978-81-265-1259-1 Online books[edit] Boelkins, M. (2012). "Active Calculus: a free, open text". Retrieved 1 Feb 2013 from http://gvsu.edu/s/kmCrowell, B. (2003). "Calculus" Light and Matter, Fullerton. Retrieved 6 May 2007 from http://www.lightandmatter.com/calc/calc.pdfGarrett, P. (2006). "Notes on first year calculus" University of Minnesota. Retrieved 6 May 2007 fromhttp://www.math.umn.edu/~garrett/calculus/first_year/notes.pdfFaraz, H. (2006). "Understanding Calculus" Retrieved 6 May 2007 from Understanding Calculus, URLhttp://www.understandingcalculus.com/ (HTML only)Keisler, H. J. (2000). "Elementary Calculus: An Approach Using Infinitesimals" Retrieved 29 August 2010 fromhttp://www.math.wisc.edu/~keisler/calc.htmlMauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology. Retrieved 6 May 2007 fromhttp://www.cacr.caltech.edu/~sean/applied_math.pdfSloughter, Dan (2000). "Difference Equations to Differential Equations: An introduction to calculus". Retrieved 17 March 2009 from http://synechism.org/drupal/de2de/Stroyan, K.D. (2004). "A brief introduction to infinitesimal calculus" University of Iowa. Retrieved 6 May 2007 fromhttp://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm(HTML only)Strang, G. (1991). "Calculus" Massachusetts Institute of Technology. Retrieved 6 May 2007 fromhttp://ocw.mit.edu/ans7870/resources/Strang/strangtext.htmSmith, William V. (2001). "The Calculus" Retrieved 4 July 2008 [1](HTML only). External links[edit]Find more about Calculus at Wikipedia'ssister projectsDefinitions and translations from WiktionaryMedia from CommonsLearning resources from WikiversityNews stories from WikinewsQuotations from WikiquoteSource texts from WikisourceTextbooks from WikibooksWeisstein, Eric W., "Calculus", MathWorld.Topics on Calculus at PlanetMathCalculus Made Easy (1914) by Silvanus P. Thompson Full text in PDFCalculus on In Our Time at the BBC. (listen now)Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sitesCOW: Calculus on the Web at Temple University – contains resources ranging from pre-calculus and associated algebraEarliest Known Uses of Some of the Words of Mathematics: Calculus & AnalysisOnline Integrator (WebMathematica) from Wolfram ResearchThe Role of Calculus in College Mathematics from ERICDigests.orgOpenCourseWare Calculus from the Massachusetts Institute of TechnologyInfinitesimal Calculus – an article on its historical development, in Encyclopedia of Mathematics, Michiel Hazewinkel ed. .Elements of Calculus I and Calculus II for Business, OpenCourseWare from the University of Notre Dame with activities, exams and interactive applets.Calculus for Beginners and Artists by Daniel Kleitman, MITCalculus Problems and Solutions by D. A. KoubaSolved problems in calculusDonald Allen's notes on calculusCalculus training materials at imomath.comVideo explanations and solved problems in calculus Raymond, CUNY[hide] vte Areas of mathematics Areas ArithmeticAlgebraelementarylinearmultilinearabstractGeometrydiscretealgebraicdifferentialfiniteTrigonometryCalculus/AnalysisFunctional analysisSet theoryLogicCategory theoryNumber theoryCombinatoricsGraph theoryTopologyLie theoryDifferential equations/Dynamical systemsMathematical physicsNumerical analysisComputationInformation theoryProbabilityMathematical statisticsMathematical optimizationControl theoryGame theoryRepresentation theory Divisions Pure mathematicsApplied mathematicsDiscrete mathematicsComputational mathematics CategoryMathematics portalOutlineLists Categories: Calculus Navigation menu Create accountLog in ArticleTalk ReadEditView history Navigation Main pageContentsFeatured contentCurrent eventsRandom articleDonate to WikipediaWikimedia Shop Interaction HelpAbout WikipediaCommunity portalRecent changesContact Wikipedia Toolbox What links hereRelated changesUpload fileSpecial pagesPermanent linkPage informationCite this page Print/export Create a bookDownload as PDFPrintable version Languages ???????????AragonésAsturianu?????Bân-lâm-gúBosanski?eskyDeutschΕλληνικάEspañolEsperanto?????FrançaisGaeilge???????????IdoBahasa IndonesiaÍslenskaItaliano?????Basa JawaLatina???????????Bahasa Melayu???Norsk nynorsk??????PolskiPortuguêsRuna Simi???????Scots?????Simple EnglishSiSwatiTagalog????????Türkçe??????????????Ti?ng Vi?tWinaray????Edit links This page was last modified on 26 June 2013 at 13:43. Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. By using this site, you agree to the Terms of Use andPrivacy Policy. Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.Privacy policyAbout WikipediaDisclaimersContact WikipediaMobile view Calculus From Wikipedia, the free encyclopedia This article is about the branch of mathematics. For other uses, see Calculus (disambiguation). CalculusFundamental theoremLimits of functionsContinuityMean value theoremRolle's theorem Differential calculus[show] Integra CalculusFrom Wikipedia, the free encyclopedia This article is about the branch of mathematics. For other uses, see Calculus (disambiguation).
Calculus is the mathematical study of change,[1] in the same way that geometry is the study of shape and algebra is the study of operations and their application to solving equations. It has two major branches, differential calculus (concerning rates of change and slopes of curves), and integral calculus (concerning accumulation of quantities and the areas under curves); these two branches are related to each other by the fundamental theorem of calculus. Both branches make use of the fundamental notions of convergenceof infinite sequences and infinite series to a well-defined limit. Calculus has widespread uses in science, economics, and engineering and can solve many problems that algebraalone cannot. Calculus is a major part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study offunctions and limits, broadly called mathematical analysis. Calculus has historically been called "the calculus of infinitesimals", or "infinitesimal calculus". The word "calculus" comes from Latin (calculus) and means a small stone used for counting. More generally, calculus (plural calculi) refers to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus,calculus of variations, lambda calculus, and process calculus.
History[edit]Main article: History of calculus Ancient[edit]The ancient period introduced some of the ideas that led to integral calculus, but does not seem to have developed these ideas in a rigorous and systematic way. Calculations of volumes and areas, one goal of integral calculus, can be found in the Egyptian Moscow papyrus (c. 1820 BC), but the formulas are simple instructions, with no indication as to method, and some of them lack major components.[2] From the age of Greek mathematics, Eudoxus (c. 408−355 BC) used the method of exhaustion, which foreshadows the concept of the limit, to calculate areas and volumes, while Archimedes (c. 287−212 BC) developed this idea further, inventingheuristics which resemble the methods of integral calculus.[3] The method of exhaustion was later reinvented in China by Liu Hui in the 3rd century AD in order to find the area of a circle.[4] In the 5th century AD, Zu Chongzhi established a method that would later be called Cavalieri's principle to find the volume of a sphere.[5] Medieval[edit]In the 14th century, Indian mathematician Madhava of Sangamagrama and the Kerala school of astronomy and mathematics stated components of calculus such as the Taylor series andinfinite series approximations.[6] Modern[edit]
In Europe, the foundational work was a treatise due to Bonaventura Cavalieri, who argued that volumes and areas should be computed as the sums of the volumes and areas of infinitesimally thin cross-sections. The ideas were similar to Archimedes' inThe Method, but this treatise was lost until the early part of the twentieth century. Cavalieri's work was not well respected since his methods could lead to erroneous results, and the infinitesimal quantities he introduced were disreputable at first. The formal study of calculus brought together Cavalieri's infinitesimals with the calculus of finite differences developed in Europe at around the same time. Pierre de Fermat, claiming that he borrowed from Diophantus, introduced the concept of adequality, which represented equality up to an infinitesimal error term.[8] The combination was achieved by John Wallis, Isaac Barrow, and James Gregory, the latter two proving the second fundamental theorem of calculus around 1670. The product rule and chain rule, the notion of higher derivatives, Taylor series, and analytical functions were introduced by Isaac Newtonin an idiosyncratic notation which he used to solve problems of mathematical physics.[9] In his works, Newton rephrased his ideas to suit the mathematical idiom of the time, replacing calculations with infinitesimals by equivalent geometrical arguments which were considered beyond reproach. He used the methods of calculus to solve the problem of planetary motion, the shape of the surface of a rotating fluid, the oblateness of the earth, the motion of a weight sliding on a cycloid, and many other problems discussed in hisPrincipia Mathematica (1687). In other work, he developed series expansions for functions, including fractional and irrational powers, and it was clear that he understood the principles of the Taylor series. He did not publish all these discoveries, and at this time infinitesimal methods were still considered disreputable.  Gottfried Wilhelm Leibniz was the first to publish his results on the development of calculus. These ideas were arranged into a true calculus of infinitesimals by Gottfried Wilhelm Leibniz, who was originally accused of plagiarism by Newton.[10] He is now regarded as an independent inventor of and contributor to calculus. His contribution was to provide a clear set of rules for working with infinitesimal quantities, allowing the computation of second and higher derivatives, and providing the product rule and chain rule, in their differential and integral forms. Unlike Newton, Leibniz paid a lot of attention to the formalism, often spending days determining appropriate symbols for concepts. Leibniz and Newton are usually both credited with the invention of calculus. Newton was the first to apply calculus to general physics and Leibniz developed much of the notation used in calculus today. The basic insights that both Newton and Leibniz provided were the laws of differentiation and integration, second and higher derivatives, and the notion of an approximating polynomial series. By Newton's time, the fundamental theorem of calculus was known. When Newton and Leibniz first published their results, there was great controversy over which mathematician (and therefore which country) deserved credit. Newton derived his results first, but Leibniz published first. Newton claimed Leibniz stole ideas from his unpublished notes, which Newton had shared with a few members of the Royal Society. This controversy divided English-speaking mathematicians from continental mathematicians for many years, to the detriment of English mathematics. A careful examination of the papers of Leibniz and Newton shows that they arrived at their results independently, with Leibniz starting first with integration and Newton with differentiation. Today, both Newton and Leibniz are given credit for developing calculus independently. It is Leibniz, however, who gave the new discipline its name. Newton called his calculus "the science of fluxions". Since the time of Leibniz and Newton, many mathematicians have contributed to the continuing development of calculus. One of the first and most complete works on finite and infinitesimal analysis was written in 1748 by Maria Gaetana Agnesi.[11] Foundations[edit]In calculus, foundations refers to the rigorous development of a subject from precise axioms and definitions. In early calculus the use of infinitesimal quantities was thought unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle and Bishop Berkeley. Berkeley famously described infinitesimals as the ghosts of departed quantities in his book The Analyst in 1734. A recent study argues that Leibnizian calculus was more solidly grounded than Berkeley's empiricist critique thereof.[12] Working out a rigorous foundation for calculus occupied mathematicians for much of the century following Newton and Leibniz and is still to some extent an active area of research today. Several mathematicians, including Maclaurin, tried to prove the soundness of using infinitesimals, but it would not be until 150 years later when, due to the work of Cauchy and Weierstrass, a way was finally found to avoid mere "notions" of infinitely small quantities. The foundations of differential and integral calculus had been laid. In Cauchy's writing, we find a broad range of foundational approaches, including a definition of continuity in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities. Bernhard Riemann used these ideas to give a precise definition of the integral. It was also during this period that the ideas of calculus were generalized to Euclidean space and the complex plane. In modern mathematics, the foundations of calculus are included in the field of real analysis, which contains full definitions and proofs of the theorems of calculus. The reach of calculus has also been greatly extended. Henri Lebesgue invented measure theory and used it to define integrals of all but the most pathological functions. Laurent Schwartz introduced Distributions, which can be used to take the derivative of any function whatsoever. Limits are not the only rigorous approach to the foundation of calculus. Another way is to use Abraham Robinson's non-standard analysis. Robinson's approach, developed in the 1960s, uses technical machinery from mathematical logic to augment the real number system with infinitesimal and infinite numbers, as in the original Newton-Leibniz conception. The resulting numbers are called hyperreal numbers, and they can be used to give a Leibniz-like development of the usual rules of calculus. Significance[edit]While some of the ideas of calculus had been developed earlier in Egypt, Greece, China, India, Iraq, Persia, and Japan, the modern use of calculus began in Europe, during the 17th century, when Isaac Newton and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to introduce its basic principles. The development of calculus was built on earlier concepts of instantaneous motion and area underneath curves. Applications of differential calculus include computations involving velocity and acceleration, the slope of a curve, and optimization. Applications of integral calculus include computations involving area, volume, arc length, center of mass, work, and pressure. More advanced applications include power series and Fourier series. Calculus is also used to gain a more precise understanding of the nature of space, time, and motion. For centuries, mathematicians and philosophers wrestled with paradoxes involving division by zero or sums of infinitely many numbers. These questions arise in the study of motion and area. The ancient Greek philosopher Zeno of Elea gave several famous examples of such paradoxes. Calculus provides tools, especially the limit and the infinite series, which resolve the paradoxes. Principles[edit]Limits and infinitesimals[edit]Calculus is usually developed by working with very small quantities. Historically, the first method of doing so was by infinitesimals. These are objects which can be treated like numbers but which are, in some sense, "infinitely small". An infinitesimal number dx could be greater than 0, but less than any number in the sequence 1, 1/2, 1/3, ... and less than any positive real number. Any integer multiple of an infinitesimal is still infinitely small, i.e., infinitesimals do not satisfy the Archimedean property. From this point of view, calculus is a collection of techniques for manipulating infinitesimals. This approach fell out of favor in the 19th century because it was difficult to make the notion of an infinitesimal precise. However, the concept was revived in the 20th century with the introduction of non-standard analysis and smooth infinitesimal analysis, which provided solid foundations for the manipulation of infinitesimals. In the 19th century, infinitesimals were replaced by limits. Limits describe the value of a function at a certain input in terms of its values at nearby input. They capture small-scale behavior, just like infinitesimals, but use the ordinary real number system. In this treatment, calculus is a collection of techniques for manipulating certain limits. Infinitesimals get replaced by very small numbers, and the infinitely small behavior of the function is found by taking the limiting behavior for smaller and smaller numbers. Limits are the easiest way to provide rigorous foundations for calculus, and for this reason they are the standard approach. Differential calculus[edit]Main article: Differential calculus Differential calculus is the study of the definition, properties, and applications of the derivative of a function. The process of finding the derivative is calleddifferentiation. Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. By finding the derivative of a function at every point in its domain, it is possible to produce a new function, called the derivative function or just thederivative of the original function. In mathematical jargon, the derivative is alinear operator which inputs a function and outputs a second function. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. (The function it produces turns out to be the doubling function.) The most common symbol for a derivative is an apostrophe-like mark called prime. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function. If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity of the ball. If a function is linear (that is, if the graph of the function is a straight line), then the function can be written as y = mx + b, where x is the independent variable, y is the dependent variable, b is the y-intercept, and: This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in ydivided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point abecause it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero: Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f. Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function.  The derivative f′(x) of a curve at a point is the slope of the line tangent to that curve at that point. This slope is determined by considering the limiting value of the slopes of secant lines. Here the function involved (drawn in red) is f(x) = x3 − x. The tangent line (in green) which passes through the point (−3/2, −15/8) has a slope of 23/4. Note that the vertical and horizontal scales in this image are different. The slope of tangent line to the squaring function at the point (3,9) is 6, that is to say, it is going up six times as fast as it is going to the right. The limit process just described can be performed for any point in the domain of the squaring function. This defines the derivative function of the squaring function, or just the derivative of the squaring function for short. A similar computation to the one above shows that the derivative of the squaring function is the doubling function. Leibniz notation[edit]Main article: Leibniz's notation A common notation, introduced by Leibniz, for the derivative in the example above is In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example: In this usage, the dx in the denominator is read as "with respect to x". Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real numbers; although it is possible to avoid such manipulations, they are sometimes notationally convenient in expressing operations such as the total derivative. Integral calculus[edit]Main article: Integral Integral calculus is the study of the definitions, properties, and applications of two related concepts, the indefinite integral and thedefinite integral. The process of finding the value of an integral is called integration. In technical language, integral calculus studies two related linear operators. The indefinite integral is the antiderivative, the inverse operation to the derivative. F is an indefinite integral of f when f is a derivative of F. (This use of lower- and upper-case letters for a function and its indefinite integral is common in calculus.) The definite integral inputs a function and outputs a number, which gives the algebraic sum of areas between the graph of the input and the x-axis. The technical definition of the definite integral is the limit of a sum of areas of rectangles, called a Riemann sum. A motivating example is the distances traveled in a given time. If the speed is constant, only multiplication is needed, but if the speed changes, then we need a more powerful method of finding the distance. One such method is to approximate the distance traveled by breaking up the time into many short intervals of time, then multiplying the time elapsed in each interval by one of the speeds in that interval, and then taking the sum (a Riemann sum) of the approximate distance traveled in each interval. The basic idea is that if only a short time elapses, then the speed will stay more or less the same. However, a Riemann sum only gives an approximation of the distance traveled. We must take the limit of all such Riemann sums to find the exact distance traveled. If f(x) in the diagram on the left represents speed as it varies over time, the distance traveled (between the times represented by a and b) is the area of the shaded region s. To approximate that area, an intuitive method would be to divide up the distance between a and b into a number of equal segments, the length of each segment represented by the symbol Δx. For each small segment, we can choose one value of the function f(x). Call that value h. Then the area of the rectangle with base Δxand height h gives the distance (time Δx multiplied by speed h) traveled in that segment. Associated with each segment is the average value of the function above it, f(x)=h. The sum of all such rectangles gives an approximation of the area between the axis and the curve, which is an approximation of the total distance traveled. A smaller value for Δx will give more rectangles and in most cases a better approximation, but for an exact answer we need to take a limit as Δxapproaches zero. The symbol of integration is and is read "the integral from a to b of f-of-x with respect to x." The Leibniz notation dx is intended to suggest dividing the area under the curve into an infinite number of rectangles, so that their width Δx becomes the infinitesimally small dx. In a formulation of the calculus based on limits, the notation is to be understood as an operator that takes a function as an input and gives a number, the area, as an output. The terminating differential, dx, is not a number, and is not being multiplied by f(x), although, serving as a reminder of the Δx limit definition, it can be treated as such in symbolic manipulations of the integral. Formally, the differential indicates the variable over which the function is integrated and serves as a closing bracket for the integration operator. The indefinite integral, or antiderivative, is written: Functions differing by only a constant have the same derivative, and it can be shown that the antiderivative of a given function is actually a family of functions differing only by a constant. Since the derivative of the function y = x² + C, where C is any constant, is y′ = 2x, the antiderivative of the latter given by: The unspecified constant C present in the indefinite integral or antiderivative is known as the constant of integration. Fundamental theorem[edit]Main article: Fundamental theorem of calculus The fundamental theorem of calculus states that differentiation and integration are inverse operations. More precisely, it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition of a definite integral, the Fundamental Theorem of Calculus provides a practical way of computing definite integrals. It can also be interpreted as a precise statement of the fact that differentiation is the inverse of integration. The Fundamental Theorem of Calculus states: If a function f is continuous on the interval [a, b ] and if F is a function whose derivative isf on the interval (a, b ), then Furthermore, for every x in the interval (a, b), This realization, made by both Newton and Leibniz, who based their results on earlier work by Isaac Barrow, was key to the massive proliferation of analytic results after their work became known. The fundamental theorem provides an algebraic method of computing many definite integrals—without performing limit processes—by finding formulas for antiderivatives. It is also a prototype solution of adifferential equation. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences. Applications[edit] The logarithmic spiral of the Nautilus shellis a classical image used to depict the growth and change related to calculus Calculus is used in every branch of the physical sciences, actuarial science, computer science, statistics, engineering, economics, business, medicine, demography, and in other fields wherever a problem can be mathematically modeled and an optimal solution is desired. It allows one to go from (non-constant) rates of change to the total change or vice versa, and many times in studying a problem we know one and are trying to find the other. Physics makes particular use of calculus; all concepts in classical mechanics andelectromagnetism are interrelated through calculus. The mass of an object of known density, the moment of inertia of objects, as well as the total energy of an object within a conservative field can be found by the use of calculus. An example of the use of calculus in mechanics is Newton's second law of motion historically stated it expressly uses the term "rate of change" which refers to the derivative saying The rate of change of momentum of a body is equal to the resultant force acting on the body and is in the same direction.Commonly expressed today as Force = Mass × acceleration, it involves differential calculus because acceleration is the time derivative of velocity or second time derivative of trajectory or spatial position. Starting from knowing how an object is accelerating, we use calculus to derive its path. Maxwell's theory of electromagnetism and Einstein's theory of general relativity are also expressed in the language of differential calculus. Chemistry also uses calculus in determining reaction rates and radioactive decay. In biology, population dynamics starts with reproduction and death rates to model population changes. Calculus can be used in conjunction with other mathematical disciplines. For example, it can be used with linear algebra to find the "best fit" linear approximation for a set of points in a domain. Or it can be used in probability theory to determine the probability of a continuous random variable from an assumed density function. In analytic geometry, the study of graphs of functions, calculus is used to find high points and low points (maxima and minima), slope, concavity and inflection points. Green's Theorem, which gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, is applied in an instrument known as a planimeter, which is used to calculate the area of a flat surface on a drawing. For example, it can be used to calculate the amount of area taken up by an irregularly shaped flower bed or swimming pool when designing the layout of a piece of property. Discrete Green's Theorem, which gives the relationship between a double integral of a function around a simple closed rectangular curveC and a linear combination of the antiderivative's values at corner points along the edge of the curve, allows fast calculation of sums of values in rectangular domains. For example, it can be used to efficiently calculate sums of rectangular domains in images, in order to rapidly extract features and detect object - see also the summed area table algorithm. In the realm of medicine, calculus can be used to find the optimal branching angle of a blood vessel so as to maximize flow. From the decay laws for a particular drug's elimination from the body, it's used to derive dosing laws. In nuclear medicine, it's used to build models of radiation transport in targeted tumor therapies. In economics, calculus allows for the determination of maximal profit by providing a way to easily calculate both marginal cost andmarginal revenue. Calculus is also used to find approximate solutions to equations; in practice it's the standard way to solve differential equations and do root finding in most applications. Examples are methods such as Newton's method, fixed point iteration, and linear approximation. For instance, spacecraft use a variation of the Euler method to approximate curved courses within zero gravity environments. See also[edit]Main article: Outline of calculus Lists[edit]
Related topics[edit]
References[edit]Notes[edit]
Books[edit]
Other resources[edit]Further reading[edit]
Online books[edit]
External links[edit]
Navigation menuNavigationToolboxPrint/exportLanguages
Series[show] Vector calculus[show] Multivariable calculus[show] Specialized calculi[show] vte Calculus is the mathematical study of change,[1] in the same way that geometry is the study of shape and algebra is the study of operations and their application to solving equations. It has two major branches, differential calculus (concerning rates of change and slopes of curves), and integral calculus (concerning accumulation of quantities and the areas under curves); these two branches are related to each other by the fundamental theorem of calculus. Both branches make use of the fundamental notions of convergenceof infinite sequences and infinite series to a well-defined limit. Calculus has widespread uses in science, economics, and engineering and can solve many problems that algebraalone cannot. Calculus is a major part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study offunctions and limits, broadly called mathematical analysis. Calculus has historically been called "the calculus of infinitesimals", or "infinitesimal calculus". The word "calculus" comes from Latin (calculus) and means a small stone used for counting. More generally, calculus (plural calculi) refers to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus,calculus of variations, lambda calculus, and process calculus. Contents [hide] 1History1.1Ancient1.2Medieval1.3Modern1.4Foundations1.5Significance2Principles2.1Limits and infinitesimals2.2Differential calculus2.3Leibniz notation2.4Integral calculus2.5Fundamental theorem3Applications4See also4.1Lists4.2Related topics5References5.1Notes5.2Books6Other resources6.1Further reading6.2Online books7External linksHistory[edit] Main article: History of calculus Ancient[edit] Isaac Newton developed the use of calculus in his laws of motion andgravitation. The ancient period introduced some of the ideas that led to integral calculus, but does not seem to have developed these ideas in a rigorous and systematic way. Calculations of volumes and areas, one goal of integral calculus, can be found in the EgyptianMoscow papyrus (c. 1820 BC), but the formulas are simple instructions, with no indication as to method, and some of them lack major components.[2] From the age of Greek mathematics, Eudoxus (c. 408−355 BC) used the method of exhaustion, which foreshadows the concept of the limit, to calculate areas and volumes, while Archimedes (c. 287−212 BC) developed this idea further, inventingheuristics which resemble the methods of integral calculus.[3] The method of exhaustion was later reinvented in China by Liu Hui in the 3rd century AD in order to find the area of a circle.[4] In the 5th century AD, Zu Chongzhi established a method that would later be called Cavalieri's principle to find the volume of a sphere.[5] Medieval[edit] In the 14th century, Indian mathematician Madhava of Sangamagrama and the Kerala school of astronomy and mathematics stated components of calculus such as the Taylor series andinfinite series approximations.[6] Modern[edit]"The calculus was the first achievement of modern mathematics and it is difficult to overestimate its importance. I think it defines more unequivocally than anything else the inception of modern mathematics, and the system of mathematical analysis, which is its logical development, still constitutes the greatest technical advance in exact thinking." —John von Neumann[7] In Europe, the foundational work was a treatise due to Bonaventura Cavalieri, who argued that volumes and areas should be computed as the sums of the volumes and areas of infinitesimally thin cross-sections. The ideas were similar to Archimedes' inThe Method, but this treatise was lost until the early part of the twentieth century. Cavalieri's work was not well respected since his methods could lead to erroneous results, and the infinitesimal quantities he introduced were disreputable at first. The formal study of calculus brought together Cavalieri's infinitesimals with the calculus of finite differences developed in Europe at around the same time. Pierre de Fermat, claiming that he borrowed from Diophantus, introduced the concept of adequality, which represented equality up to an infinitesimal error term.[8] The combination was achieved by John Wallis, Isaac Barrow, and James Gregory, the latter two proving the second fundamental theorem of calculus around 1670. The product rule and chain rule, the notion of higher derivatives, Taylor series, and analytical functions were introduced by Isaac Newtonin an idiosyncratic notation which he used to solve problems of mathematical physics.[9] In his works, Newton rephrased his ideas to suit the mathematical idiom of the time, replacing calculations with infinitesimals by equivalent geometrical arguments which were considered beyond reproach. He used the methods of calculus to solve the problem of planetary motion, the shape of the surface of a rotating fluid, the oblateness of the earth, the motion of a weight sliding on a cycloid, and many other problems discussed in hisPrincipia Mathematica (1687). In other work, he developed series expansions for functions, including fractional and irrational powers, and it was clear that he understood the principles of the Taylor series. He did not publish all these discoveries, and at this time infinitesimal methods were still considered disreputable. Gottfried Wilhelm Leibniz was the first to publish his results on the development of calculus. These ideas were arranged into a true calculus of infinitesimals by Gottfried Wilhelm Leibniz, who was originally accused of plagiarism by Newton.[10] He is now regarded as an independent inventor of and contributor to calculus. His contribution was to provide a clear set of rules for working with infinitesimal quantities, allowing the computation of second and higher derivatives, and providing the product rule and chain rule, in their differential and integral forms. Unlike Newton, Leibniz paid a lot of attention to the formalism, often spending days determining appropriate symbols for concepts. Leibniz and Newton are usually both credited with the invention of calculus. Newton was the first to apply calculus to general physics and Leibniz developed much of the notation used in calculus today. The basic insights that both Newton and Leibniz provided were the laws of differentiation and integration, second and higher derivatives, and the notion of an approximating polynomial series. By Newton's time, the fundamental theorem of calculus was known. When Newton and Leibniz first published their results, there was great controversy over which mathematician (and therefore which country) deserved credit. Newton derived his results first, but Leibniz published first. Newton claimed Leibniz stole ideas from his unpublished notes, which Newton had shared with a few members of the Royal Society. This controversy divided English-speaking mathematicians from continental mathematicians for many years, to the detriment of English mathematics. A careful examination of the papers of Leibniz and Newton shows that they arrived at their results independently, with Leibniz starting first with integration and Newton with differentiation. Today, both Newton and Leibniz are given credit for developing calculus independently. It is Leibniz, however, who gave the new discipline its name. Newton called his calculus "the science of fluxions". Since the time of Leibniz and Newton, many mathematicians have contributed to the continuing development of calculus. One of the first and most complete works on finite and infinitesimal analysis was written in 1748 by Maria Gaetana Agnesi.[11] Maria Gaetana Agnesi Foundations[edit] In calculus, foundations refers to the rigorous development of a subject from precise axioms and definitions. In early calculus the use of infinitesimal quantities was thought unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle and Bishop Berkeley. Berkeley famously described infinitesimals as the ghosts of departed quantities in his book The Analyst in 1734. A recent study argues that Leibnizian calculus was more solidly grounded than Berkeley's empiricist critique thereof.[12] Working out a rigorous foundation for calculus occupied mathematicians for much of the century following Newton and Leibniz and is still to some extent an active area of research today. Several mathematicians, including Maclaurin, tried to prove the soundness of using infinitesimals, but it would not be until 150 years later when, due to the work of Cauchy and Weierstrass, a way was finally found to avoid mere "notions" of infinitely small quantities. The foundations of differential and integral calculus had been laid. In Cauchy's writing, we find a broad range of foundational approaches, including a definition of continuity in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities. Bernhard Riemann used these ideas to give a precise definition of the integral. It was also during this period that the ideas of calculus were generalized to Euclidean space and the complex plane. In modern mathematics, the foundations of calculus are included in the field of real analysis, which contains full definitions and proofs of the theorems of calculus. The reach of calculus has also been greatly extended. Henri Lebesgue invented measure theory and used it to define integrals of all but the most pathological functions. Laurent Schwartz introduced Distributions, which can be used to take the derivative of any function whatsoever. Limits are not the only rigorous approach to the foundation of calculus. Another way is to use Abraham Robinson's non-standard analysis. Robinson's approach, developed in the 1960s, uses technical machinery from mathematical logic to augment the real number system with infinitesimal and infinite numbers, as in the original Newton-Leibniz conception. The resulting numbers are called hyperreal numbers, and they can be used to give a Leibniz-like development of the usual rules of calculus. Significance[edit] While some of the ideas of calculus had been developed earlier in Egypt, Greece, China, India, Iraq, Persia, and Japan, the modern use of calculus began in Europe, during the 17th century, when Isaac Newton and Gottfried Wilhelm Leibniz built on the work of earlier mathematicians to introduce its basic principles. The development of calculus was built on earlier concepts of instantaneous motion and area underneath curves. Applications of differential calculus include computations involving velocity and acceleration, the slope of a curve, and optimization. Applications of integral calculus include computations involving area, volume, arc length, center of mass, work, and pressure. More advanced applications include power series and Fourier series. Calculus is also used to gain a more precise understanding of the nature of space, time, and motion. For centuries, mathematicians and philosophers wrestled with paradoxes involving division by zero or sums of infinitely many numbers. These questions arise in the study of motion and area. The ancient GreekphilosopherZeno of Elea gave several famous examples of such paradoxes. Calculus provides tools, especially the limit and the infinite series, which resolve the paradoxes. Principles[edit]Limits and infinitesimals[edit] Main articles: Limit of a function, Infinitesimal, and Infinitesimal Calculus Calculus is usually developed by working with very small quantities. Historically, the first method of doing so was by infinitesimals. These are objects which can be treated like numbers but which are, in some sense, "infinitely small". An infinitesimal number dx could be greater than 0, but less than any number in the sequence 1, 1/2, 1/3, ... and less than any positive real number. Any integer multiple of an infinitesimal is still infinitely small, i.e., infinitesimals do not satisfy the Archimedean property. From this point of view, calculus is a collection of techniques for manipulating infinitesimals. This approach fell out of favor in the 19th century because it was difficult to make the notion of an infinitesimal precise. However, the concept was revived in the 20th century with the introduction of non-standard analysis and smooth infinitesimal analysis, which provided solid foundations for the manipulation of infinitesimals. In the 19th century, infinitesimals were replaced by limits. Limits describe the value of a function at a certain input in terms of its values at nearby input. They capture small-scale behavior, just like infinitesimals, but use the ordinary real number system. In this treatment, calculus is a collection of techniques for manipulating certain limits. Infinitesimals get replaced by very small numbers, and the infinitely small behavior of the function is found by taking the limiting behavior for smaller and smaller numbers. Limits are the easiest way to provide rigorous foundations for calculus, and for this reason they are the standard approach. Differential calculus[edit] Main article: Differential calculus Tangent line at (x, f(x)). The derivative f′(x) of a curve at a point is the slope (rise over run) of the line tangent to that curve at that point. Differential calculus is the study of the definition, properties, and applications of the derivative of a function. The process of finding the derivative is calleddifferentiation. Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. By finding the derivative of a function at every point in its domain, it is possible to produce a new function, called the derivative function or just thederivative of the original function. In mathematical jargon, the derivative is alinear operator which inputs a function and outputs a second function. This is more abstract than many of the processes studied in elementary algebra, where functions usually input a number and output another number. For example, if the doubling function is given the input three, then it outputs six, and if the squaring function is given the input three, then it outputs nine. The derivative, however, can take the squaring function as an input. This means that the derivative takes all the information of the squaring function—such as that two is sent to four, three is sent to nine, four is sent to sixteen, and so on—and uses this information to produce another function. (The function it produces turns out to be the doubling function.) The most common symbol for a derivative is an apostrophe-like mark called prime. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function. If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity of the ball. If a function is linear (that is, if the graph of the function is a straight line), then the function can be written as y = mx + b, where x is the independent variable, y is the dependent variable, b is the y-intercept, and: This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in ydivided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point abecause it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero: Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f. Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function. The derivative f′(x) of a curve at a point is the slope of the line tangent to that curve at that point. This slope is determined by considering the limiting value of the slopes of secant lines. Here the function involved (drawn in red) is f(x) = x3 − x. The tangent line (in green) which passes through the point (−3/2, −15/8) has a slope of 23/4. Note that the vertical and horizontal scales in this image are different. The slope of tangent line to the squaring function at the point (3,9) is 6, that is to say, it is going up six times as fast as it is going to the right. The limit process just described can be performed for any point in the domain of the squaring function. This defines the derivative function of the squaring function, or just the derivative of the squaring function for short. A similar computation to the one above shows that the derivative of the squaring function is the doubling function. Leibniz notation[edit] Main article: Leibniz's notation A common notation, introduced by Leibniz, for the derivative in the example above is In an approach based on limits, the symbol dy/dx is to be interpreted not as the quotient of two numbers but as a shorthand for the limit computed above. Leibniz, however, did intend it to represent the quotient of two infinitesimally small numbers, dy being the infinitesimally small change in y caused by an infinitesimally small change dx applied to x. We can also think of d/dx as a differentiation operator, which takes a function as an input and gives another function, the derivative, as the output. For example: In this usage, the dx in the denominator is read as "with respect to x". Even when calculus is developed using limits rather than infinitesimals, it is common to manipulate symbols like dx and dy as if they were real numbers; although it is possible to avoid such manipulations, they are sometimes notationally convenient in expressing operations such as the total derivative. Integral calculus[edit] Main article: Integral Integral calculus is the study of the definitions, properties, and applications of two related concepts, the indefinite integral and thedefinite integral. The process of finding the value of an integral is called integration. In technical language, integral calculus studies two related linear operators. The indefinite integral is the antiderivative, the inverse operation to the derivative. F is an indefinite integral of f when f is a derivative of F. (This use of lower- and upper-case letters for a function and its indefinite integral is common in calculus.) The definite integral inputs a function and outputs a number, which gives the algebraic sum of areas between the graph of the input and the x-axis. The technical definition of the definite integral is the limit of a sum of areas of rectangles, called a Riemann sum. A motivating example is the distances traveled in a given time. If the speed is constant, only multiplication is needed, but if the speed changes, then we need a more powerful method of finding the distance. One such method is to approximate the distance traveled by breaking up the time into many short intervals of time, then multiplying the time elapsed in each interval by one of the speeds in that interval, and then taking the sum (a Riemann sum) of the approximate distance traveled in each interval. The basic idea is that if only a short time elapses, then the speed will stay more or less the same. However, a Riemann sum only gives an approximation of the distance traveled. We must take the limit of all such Riemann sums to find the exact distance traveled. Integration can be thought of as measuring the area under a curve, defined by f(x), between two points (here a and b). If f(x) in the diagram on the left represents speed as it varies over time, the distance traveled (between the times represented by a and b) is the area of the shaded region s. To approximate that area, an intuitive method would be to divide up the distance between a and b into a number of equal segments, the length of each segment represented by the symbol Δx. For each small segment, we can choose one value of the function f(x). Call that value h. Then the area of the rectangle with base Δxand height h gives the distance (time Δx multiplied by speed h) traveled in that segment. Associated with each segment is the average value of the function above it, f(x)=h. The sum of all such rectangles gives an approximation of the area between the axis and the curve, which is an approximation of the total distance traveled. A smaller value for Δx will give more rectangles and in most cases a better approximation, but for an exact answer we need to take a limit as Δxapproaches zero. The symbol of integration is , an elongated S (the S stands for "sum"). The definite integral is written as: and is read "the integral from a to b of f-of-x with respect to x." The Leibniz notation dx is intended to suggest dividing the area under the curve into an infinite number of rectangles, so that their width Δx becomes the infinitesimally small dx. In a formulation of the calculus based on limits, the notation is to be understood as an operator that takes a function as an input and gives a number, the area, as an output. The terminating differential, dx, is not a number, and is not being multiplied by f(x), although, serving as a reminder of the Δx limit definition, it can be treated as such in symbolic manipulations of the integral. Formally, the differential indicates the variable over which the function is integrated and serves as a closing bracket for the integration operator. The indefinite integral, or antiderivative, is written: Functions differing by only a constant have the same derivative, and it can be shown that the antiderivative of a given function is actually a family of functions differing only by a constant. Since the derivative of the function y = x² + C, where C is any constant, is y′ = 2x, the antiderivative of the latter given by: The unspecified constant C present in the indefinite integral or antiderivative is known as the constant of integration. Fundamental theorem[edit] Main article: Fundamental theorem of calculus The fundamental theorem of calculus states that differentiation and integration are inverse operations. More precisely, it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition of a definite integral, the Fundamental Theorem of Calculus provides a practical way of computing definite integrals. It can also be interpreted as a precise statement of the fact that differentiation is the inverse of integration. The Fundamental Theorem of Calculus states: If a function f is continuous on the interval [a, b ] and if F is a function whose derivative isf on the interval (a, b ), then Furthermore, for every x in the interval (a, b), This realization, made by both Newton and Leibniz, who based their results on earlier work by Isaac Barrow, was key to the massive proliferation of analytic results after their work became known. The fundamental theorem provides an algebraic method of computing many definite integrals—without performing limit processes—by finding formulas for antiderivatives. It is also a prototype solution of adifferential equation. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences. Applications[edit] The logarithmic spiral of the Nautilus shellis a classical image used to depict the growth and change related to calculus Calculus is used in every branch of the physical sciences, actuarial science, computer science, statistics, engineering, economics, business, medicine, demography, and in other fields wherever a problem can be mathematically modeled and an optimal solution is desired. It allows one to go from (non-constant) rates of change to the total change or vice versa, and many times in studying a problem we know one and are trying to find the other. Physics makes particular use of calculus; all concepts in classical mechanics andelectromagnetism are interrelated through calculus. The mass of an object of known density, the moment of inertia of objects, as well as the total energy of an object within a conservative field can be found by the use of calculus. An example of the use of calculus in mechanics is Newton's second law of motion: historically stated it expressly uses the term "rate of change" which refers to the derivative saying Therate of changeof momentum of a body is equal to the resultant force acting on the body and is in the same direction.Commonly expressed today as Force = Mass × acceleration, it involves differential calculus because acceleration is the time derivative of velocity or second time derivative of trajectory or spatial position. Starting from knowing how an object is accelerating, we use calculus to derive its path. Maxwell's theory of electromagnetism and Einstein's theory of general relativity are also expressed in the language of differential calculus. Chemistry also uses calculus in determining reaction rates and radioactive decay. In biology, population dynamics starts with reproduction and death rates to model population changes. Calculus can be used in conjunction with other mathematical disciplines. For example, it can be used with linear algebra to find the "best fit" linear approximation for a set of points in a domain. Or it can be used in probability theory to determine the probability of a continuous random variable from an assumed density function. In analytic geometry, the study of graphs of functions, calculus is used to find high points and low points (maxima and minima), slope, concavity and inflection points. Green's Theorem, which gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C, is applied in an instrument known as a planimeter, which is used to calculate the area of a flat surface on a drawing. For example, it can be used to calculate the amount of area taken up by an irregularly shaped flower bed or swimming pool when designing the layout of a piece of property. Discrete Green's Theorem, which gives the relationship between a double integral of a function around a simple closed rectangular curveC and a linear combination of the antiderivative's values at corner points along the edge of the curve, allows fast calculation of sums of values in rectangular domains. For example, it can be used to efficiently calculate sums of rectangular domains in images, in order to rapidly extract features and detect object - see also the summed area table algorithm. In the realm of medicine, calculus can be used to find the optimal branching angle of a blood vessel so as to maximize flow. From the decay laws for a particular drug's elimination from the body, it's used to derive dosing laws. In nuclear medicine, it's used to build models of radiation transport in targeted tumor therapies. In economics, calculus allows for the determination of maximal profit by providing a way to easily calculate both marginal cost andmarginal revenue. Calculus is also used to find approximate solutions to equations; in practice it's the standard way to solve differential equations and do root finding in most applications. Examples are methods such as Newton's method, fixed point iteration, and linear approximation. For instance, spacecraft use a variation of the Euler method to approximate curved courses within zero gravity environments. See also[edit] Mathematics portalAnalysis portal Main article: Outline of calculus Lists[edit]List of calculus topicsList of derivatives and integrals in alternative calculiList of differentiation identitiesPublications in calculusTable of integralsRelated topics[edit]Calculus of finite differencesCalculus with polynomialsComplex analysisDifferential equationDifferential geometryElementary Calculus: An Infinitesimal ApproachFourier seriesIntegral equationMathematical analysisMultivariable calculusNon-classical analysisNon-standard analysisNon-standard calculusPrecalculus (mathematical education)Product integralStochastic calculusTaylor seriesReferences[edit]Notes[edit] ^Latorre, Donald R.; Kenelly, John W.; Reed, Iris B.; Biggers, Sherry (2007), Calculus Concepts: An Applied Approach to the Mathematics of Change, Cengage Learning, p. 2, ISBN0-618-78981-2, Chapter 1, p 2^Morris Kline, Mathematical thought from ancient to modern times, Vol. I^Archimedes, Method, in The Works of ArchimedesISBN 978-0-521-66160-7^Dun, Liu; Fan, Dainian; Cohen, Robert Sonné (1966). A comparison of Archimdes' and Liu Hui's studies of circles. Chinese studies in the history and philosophy of science and technology 130. Springer. p. 279. ISBN0-7923-3463-9., Chapter , p. 279^Zill, Dennis G.; Wright, Scott; Wright, Warren S. (2009).Calculus: Early Transcendentals (3 ed.). Jones & Bartlett Learning. p. xxvii. ISBN0-7637-5995-3., Extract of page 27^http://www-history.mcs.st-andrews.ac.uk/HistTopics/Indian_mathematics.html^von Neumann, J., "The Mathematician", in Heywood, R. B., ed.,The Works of the Mind, University of Chicago Press, 1947, pp. 180–196. Reprinted in Bródy, F., Vámos, T., eds., The Neumann Compedium, World Scientific Publishing Co. Pte. Ltd., 1995,ISBN 981-02-2201-7, pp. 618–626.^André Weil: Number theory. An approach through history. From Hammurapi to Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0-8176-4565-9, p. 28.^Donald Allen: Calculus,http://www.math.tamu.edu/~dallen/history/calc1/calc1.html^Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscr Books[edit] Larson, Ron, Bruce H. Edwards (2010). "Calculus", 9th ed., Brooks Cole Cengage Learning. ISBN 978-0-547-16702-2McQuarrie, Donald A. (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 978-1-891389-24-5Stewart, James (2008). Calculus: Early Transcendentals, 6th ed., Brooks Cole Cengage Learning. ISBN 978-0-495-01166-8Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano (2008), "Calculus", 11th ed., Addison-Wesley. ISBN 0-321-48987-X Other resources[edit]Further reading[edit] Boyer, Carl Benjamin (1949). The History of the Calculus and its Conceptual Development. Hafner. Dover edition 1959, ISBN 0-486-60509-4Courant, RichardISBN 978-3-540-65058-4Introduction to calculus and analysis 1.Edmund Landau. ISBN 0-8218-2830-4Differential and Integral Calculus, American Mathematical Society.Robert A. Adams. (1999). ISBN 978-0-201-39607-2Calculus: A complete course.Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7.John Lane Bell: A Primer of Infinitesimal Analysis, Cambridge University Press, 1998. ISBN 978-0-521-62401-5. Uses synthetic differential geometry and nilpotent infinitesimals.Florian Cajori, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), pp. 1–46.Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton Univ. Press, 2004.Cliff Pickover. (2003). ISBN 978-0-471-26987-8Calculus and Pizza: A Math Cookbook for the Hungry Mind.Michael Spivak. (September 1994). ISBN 978-0-914098-89-8Calculus. Publish or Perish publishing.Tom M. Apostol. (1967). ISBN 978-0-471-00005-1Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley.Tom M. Apostol. (1969). ISBN 978-0-471-00007-5Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley.Silvanus P. Thompson and Martin Gardner. (1998). ISBN 978-0-312-18548-0Calculus Made Easy.Mathematical Association of America. (1988). Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.Thomas/Finney. (1996). ISBN 978-0-201-53174-9Calculus and Analytic geometry 9th, Addison Wesley.Weisstein, Eric W. "Second Fundamental Theorem of Calculus."From MathWorld—A Wolfram Web Resource.Howard Anton,Irl Bivens,Stephen Davis:"Calculus",John Willey and Sons Pte. Ltd.,2002.ISBN 978-81-265-1259-1 Online books[edit] Boelkins, M. (2012). "Active Calculus: a free, open text". Retrieved 1 Feb 2013 from http://gvsu.edu/s/kmCrowell, B. (2003). "Calculus" Light and Matter, Fullerton. Retrieved 6 May 2007 from http://www.lightandmatter.com/calc/calc.pdfGarrett, P. (2006). "Notes on first year calculus" University of Minnesota. Retrieved 6 May 2007 fromhttp://www.math.umn.edu/~garrett/calculus/first_year/notes.pdfFaraz, H. (2006). "Understanding Calculus" Retrieved 6 May 2007 from Understanding Calculus, URLhttp://www.understandingcalculus.com/ (HTML only)Keisler, H. J. (2000). "Elementary Calculus: An Approach Using Infinitesimals" Retrieved 29 August 2010 fromhttp://www.math.wisc.edu/~keisler/calc.htmlMauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology. Retrieved 6 May 2007 fromhttp://www.cacr.caltech.edu/~sean/applied_math.pdfSloughter, Dan (2000). "Difference Equations to Differential Equations: An introduction to calculus". Retrieved 17 March 2009 from http://synechism.org/drupal/de2de/Stroyan, K.D. (2004). "A brief introduction to infinitesimal calculus" University of Iowa. Retrieved 6 May 2007 fromhttp://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm(HTML only)Strang, G. (1991). "Calculus" Massachusetts Institute of Technology. Retrieved 6 May 2007 fromhttp://ocw.mit.edu/ans7870/resources/Strang/strangtext.htmSmith, William V. (2001). "The Calculus" Retrieved 4 July 2008 [1](HTML only). External links[edit]Find more about Calculus at Wikipedia'ssister projectsDefinitions and translations from WiktionaryMedia from CommonsLearning resources from WikiversityNews stories from WikinewsQuotations from WikiquoteSource texts from WikisourceTextbooks from WikibooksWeisstein, Eric W., "Calculus", MathWorld.Topics on Calculus at PlanetMathCalculus Made Easy (1914) by Silvanus P. Thompson Full text in PDFCalculus on In Our Time at the BBC. (listen now)Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sitesCOW: Calculus on the Web at Temple University – contains resources ranging from pre-calculus and associated algebraEarliest Known Uses of Some of the Words of Mathematics: Calculus & AnalysisOnline Integrator (WebMathematica) from Wolfram ResearchThe Role of Calculus in College Mathematics from ERICDigests.orgOpenCourseWare Calculus from the Massachusetts Institute of TechnologyInfinitesimal Calculus – an article on its historical development, in Encyclopedia of Mathematics, Michiel Hazewinkel ed. .Elements of Calculus I and Calculus II for Business, OpenCourseWare from the University of Notre Dame with activities, exams and interactive applets.Calculus for Beginners and Artists by Daniel Kleitman, MITCalculus Problems and Solutions by D. A. KoubaSolved problems in calculusDonald Allen's notes on calculusCalculus training materials at imomath.comVideo explanations and solved problems in calculus Raymond, CUNY[hide] vte Areas of mathematics Areas ArithmeticAlgebraelementarylinearmultilinearabstractGeometrydiscretealgebraicdifferentialfiniteTrigonometryCalculus/AnalysisFunctional analysisSet theoryLogicCategory theoryNumber theoryCombinatoricsGraph theoryTopologyLie theoryDifferential equations/Dynamical systemsMathematical physicsNumerical analysisComputationInformation theoryProbabilityMathematical statisticsMathematical optimizationControl theoryGame theoryRepresentation theory Divisions Pure mathematicsApplied mathematicsDiscrete mathematicsComputational mathematics CategoryMathematics portalOutlineLists Categories: Calculus Navigation menu Create accountLog in ArticleTalk ReadEditView history Navigation Main pageContentsFeatured contentCurrent eventsRandom articleDonate to WikipediaWikimedia Shop Interaction HelpAbout WikipediaCommunity portalRecent changesContact Wikipedia Toolbox What links hereRelated changesUpload fileSpecial pagesPermanent linkPage informationCite this page Print/export Create a bookDownload as PDFPrintable version Languages ???????????AragonésAsturianu?????Bân-lâm-gúBosanski?eskyDeutschΕλληνικάEspañolEsperanto?????FrançaisGaeilge???????????IdoBahasa IndonesiaÍslenskaItaliano?????Basa JawaLatina???????????Bahasa Melayu???Norsk nynorsk??????PolskiPortuguêsRuna Simi???????Scots?????Simple EnglishSiSwatiTagalog????????Türkçe??????????????Ti?ng Vi?tWinaray????Edit links This page was last modified on 26 June 2013 at 13:43. Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. By using this site, you agree to the Terms of Use andPrivacy Policy. Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.Privacy policyAbout WikipediaDisclaimersContact WikipediaMobile view | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Affected by 'Laziness Syndrome'
Registered: 08-22-12
Location: counter strike global offensive
Last Post: 3389 days
Last Active: 2994 days
07-02-13 07:17 AM
 Barathemos is Offline
| ID: 831563 | 34 Words
Barathemos is Offline
| ID: 831563 | 34 Words
 Barathemos is Offline
Barathemos is Offline

POSTS: 2761/15635
POST EXP: 668938
LVL EXP: 124855298
CP: 46550.1
VIZ: 892425

zelda2 : Um. What? Why would you do that? Why did you copy paste a page on calculus from Wikipedia? It doesn't seem like something you would do. Local Mods : Could you edit this out? Local Mods : Could you edit this out? |
Minecraft Admin
Affected by 'Laziness Syndrome'
Registered: 02-17-13
Location: Atlanta, Georgia
Last Post: 20 days
Last Active: 2 days
07-02-13 08:10 AM
 Tails the Fox is Offline
| ID: 831637 | 18 Words
Tails the Fox is Offline
| ID: 831637 | 18 Words
 Tails the Fox is Offline
Tails the Fox is Offline

POSTS: 1852/2501
POST EXP: 108718
LVL EXP: 9254131
CP: 8686.1
VIZ: 86206

 Vizzed #1 Castlevania Fan. Vizzed #1 British Furry |
Affected by 'Laziness Syndrome'
Registered: 04-24-09
Location: England
Last Post: 3419 days
Last Active: 3380 days
07-02-13 08:45 AM
 zelda2 is Offline
| ID: 831678 | 11 Words
zelda2 is Offline
| ID: 831678 | 11 Words
 zelda2 is Offline
zelda2 is Offline

POSTS: 1467/1763
POST EXP: -40107
LVL EXP: 4830509
CP: 1466.9
VIZ: 9987

Tails the Fox : I get an error when I try to |
Affected by 'Laziness Syndrome'
Registered: 08-22-12
Location: counter strike global offensive
Last Post: 3389 days
Last Active: 2994 days
07-02-13 01:33 PM
 DittoDude44 is Offline
| ID: 832153 | 12 Words
DittoDude44 is Offline
| ID: 832153 | 12 Words
 DittoDude44 is Offline
DittoDude44 is Offline

POSTS: 839/2065
POST EXP: 72735
LVL EXP: 6085763
CP: 2675.4
VIZ: 15811

| The Birthday Thread Maker |
Affected by 'Laziness Syndrome'
Registered: 10-13-12
Last Post: 3822 days
Last Active: 3821 days
07-02-13 01:39 PM
 linkmaster99 is Offline
| ID: 832168 | 118 Words
linkmaster99 is Offline
| ID: 832168 | 118 Words
 linkmaster99 is Offline
linkmaster99 is Offline

POSTS: 385/732
POST EXP: 65659
LVL EXP: 1248944
CP: 3593.6
VIZ: 24474

I totally agree Pokémon tower defence is a amazing game series. Did you all here about the Pokémon Tower defence 2 version. They are in the Johto region, and they made it sort of like a real Pokémon game where you can walk around, and talk to other people. You can also, walk with your Pokémon out of it's pokeball. Pokémon Tower Defence is a really amazing game that never fail to surprise me. I would never be on vizzed right this instant, but since Pokémon Tower Defence 2 isn't fully completed yet I intend to wait while I can. I haven't been on it in a few months. Still though awesome flash game I love it |
I linkmaster99 is vizzed NO.1 zelda fan  |
Affected by 'Laziness Syndrome'
Registered: 05-30-13
Location: Think about me. Ill be there >
Last Post: 3844 days
Last Active: 3843 days
07-02-13 05:29 PM
 Batcake is Offline
| ID: 832463 | 30 Words
Batcake is Offline
| ID: 832463 | 30 Words
 Batcake is Offline
Batcake is Offline
Black Bot

POSTS: 1066/3246
POST EXP: 146939
LVL EXP: 11988120
CP: 5867.6
VIZ: 3347

OMG! This game was just legendary! This game is amazing and I am already half way through it! This game is very addicting, challenging, and just too awesome and amazing! |
| hi |
Affected by 'Laziness Syndrome'
Registered: 10-17-12
Location: US
Last Post: 764 days
Last Active: 144 days
Page Comments
This page has no comments


 User Notice
User Notice 


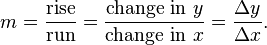
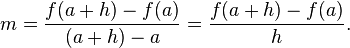
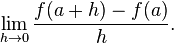
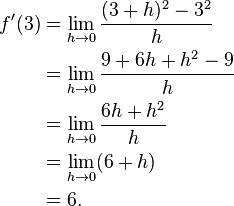


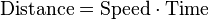

 , an elongated S (the S stands for "sum"). The definite integral is written as:
, an elongated S (the S stands for "sum"). The definite integral is written as: